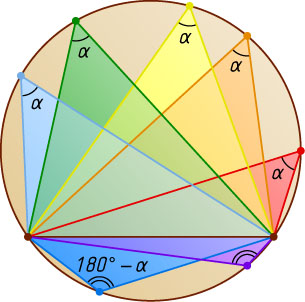
1. Докажите, что вписанный угол равен половине соответствующего центрального угла (или дуги) окружности.
Указание. Разберите три случая: центр окружности лежит на стороне угла, внутри угла, вне угла.
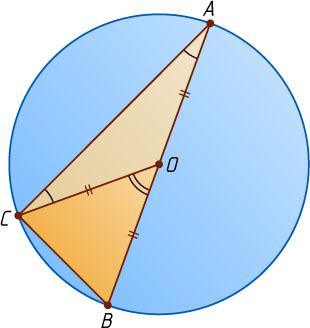
Решение. Пусть центр O
окружности лежит на стороне AB
вписанного угла BAC
(рис. 1). Поскольку BOC
— внешний угол равнобедренного треугольника AOC
, то
\angle BOC=\angle BAC+\angle ACO=2\angle BAC.
Следовательно,
\angle BAC=\frac{1}{2}\angle BOC,
т. е. вписанный угол BAC
равен половине центрального угла BOC
, или половине дуги BC
, не содержащей точки A
.
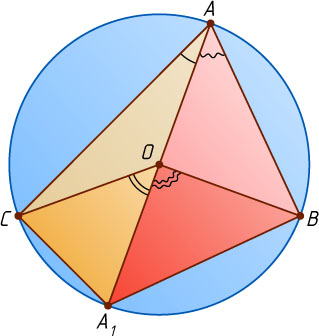
Пусть центр окружности лежит между сторонами вписанного угла BAC
(рис. 2). Проведём диаметр AA_{1}
. Тогда луч AA_{1}
лежит между сторонами угла BAC
. Поэтому
\angle BAC=\angle BAA_{1}+\angle CAA_{1}.
Поскольку центр окружности лежит на общей стороне вписанных углов BAA_{1}
и CAA_{1}
, то по доказанному
\angle BAA_{1}=\frac{1}{2}\angle BOA_{1},~\angle CAA_{1}=\frac{1}{2}\angle COA_{1}.
Следовательно,
\angle BAC=\frac{1}{2}\angle BOA_{1}+\frac{1}{2}\angle COA_{1}=\frac{1}{2}(\angle BOA_{1}+\angle COA_{1})=\frac{1}{2}\angle BOC.
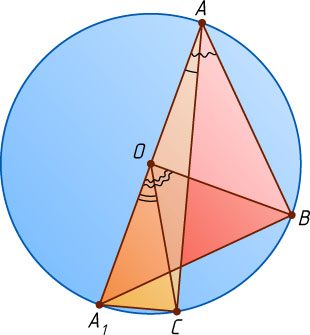
Наконец, пусть центр окружности лежит вне угла BAC
(рис. 3). Если при этом луч AC
проходит между сторонами угла BAA_{1}
, то
\angle BAC=\angle BAA_{1}-\angle CAA_{1}=\frac{1}{2}\angle BOA_{1}-\frac{1}{2}\angle COA_{1}=
=\frac{1}{2}(\angle BOA_{1}-\angle COA_{1})=\frac{1}{2}\angle BOC.
Примечание. Следствие. Вписанные в окружность углы, опирающиеся на одну хорду, равны, если их вершины расположены по одну сторону от этой хорды, и составляют в сумме 180^{\circ}
в противном случае.