132. Четырёхугольник ABCD
, диагонали которого взаимно перпендикулярны, вписан в окружность с центром O
. Докажите, что ломаная AOC
делит его на две равновеликие части.
Указание. Диаметр, перпендикулярный хорде, делит её пополам.
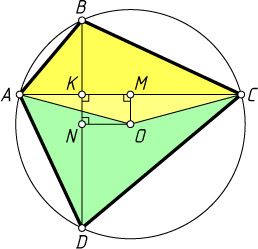
Решение. Первый способ. Пусть K
— точка пересечения диагоналей AC
и BD
. Если O
принадлежит AC
или BD
, то решение очевидно. Иначе, один из получившихся четырёхугольников — выпуклый. Будем считать что это четырёхугольник ABCO
.
Пусть тогда M
и N
— основания перпендикуляров, опущенных из точки O
на AC
и BD
(рис. 1). Тогда
S_{ABCO}=\frac{1}{2}AC\cdot OM+\frac{1}{2}AC\cdot BK=\frac{1}{2}AC\cdot(OM+BK)=
=\frac{1}{2}AC\cdot(KN+BK)=\frac{1}{4}AC\cdot BD=\frac{1}{2}S_{ABCD}.
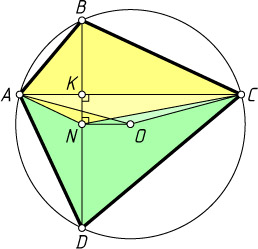
Второй способ. Поскольку ON\parallel AC
, треугольник ANC
равновелик треугольнику AOC
(рис. 2), поэтому S_{ABCO}=S_{ABCN}
, а так как AN
и CN
— медианы треугольников ABD
и CBD
, то
S_{ABCO}=\frac{1}{2}S_{\triangle ABD}+\frac{1}{2}S_{\triangle CBD}=\frac{1}{2}(S_{\triangle ABD}+S_{\triangle CBD})=\frac{1}{2}S_{ABCD}.
Примечание. Для любого выпуклого четырёхугольника ABCD
с перпендикулярными диагоналями (не обязательно вписанного) верно утверждение: если O
— точка внутри четырёхугольника, лежащая на серединном перпендикуляре к диагонали BD
, то ломаная AOC
разбивает четырёхугольник на две равновеликие части.

