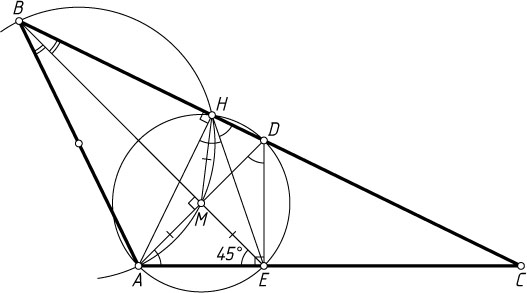
156. В треугольнике ABC
проведены высота AH
и биссектриса BE
. Известно, что \angle BEA=45^{\circ}
. Докажите, что \angle EHC=45^{\circ}
.
Указание. Через точку E
проведите прямую, перпендикулярную стороне AC
, до пересечения со стороной BC
в точке D
. Тогда DE=AE
и точки H
, D
, E
и A
лежат на одной окружности.
Решение. Первый способ. Проведём из точки E
перпендикуляр ED
к прямой AC
. Пусть D
— точка его пересечения со стороной BC
. Тогда \angle BED=45^{\circ}
. Поэтому треугольник ABE
равен треугольнику DBE
по стороне и двум прилежащим к ней углам. Значит, DE=AE
.
Из точек E
и H
отрезок AD
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AD
. Вписанные в эту окружность углы EHD
и EAD
опираются на одну и ту же дугу. При этом \angle ADE=\angle DAE=45^{\circ}
как углы при основании равнобедренного прямоугольного треугольника AED
. Следовательно,
\angle EHC=\angle EHD=\angle DAE=45^{\circ}.
Второй способ. Опустим из вершины A
перпендикуляр AM
на BE
. Треугольник AME
равнобедренный прямоугольный. Точки M
и H
лежат на окружности с диаметром AB
, значит, MH=MA=ME
(на дуги AM
и MH
опираются равные углы). Поэтому M
— центр описанной окружности треугольника AHE
. Тогда AME
— центральный угол этой окружности, значит,
\angle AHE=\frac{1}{2}\angle AME=\frac{1}{2}\cdot90^{\circ}=45^{\circ}.
Следовательно,
\angle EHC=90^{\circ}-\angle AHE=45^{\circ}.