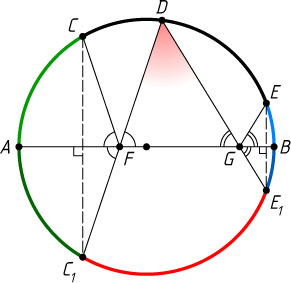
238. AB
— диаметр окружности; C
, D
, E
— точки на одной полуокружности ACDEB
. На диаметре AB
взяты: точка F
так, что \angle CFA=\angle DFB
, и точка G
так, что \angle DGA=\angle EGB
. Найдите \angle FDG
, если дуга AC
равна 60^{\circ}
, а дуга BE
равна 20^{\circ}
.
Ответ. 50^{\circ}
.
Указание. Обозначим через C_{1}
и E_{1}
точки пересечения лучей DF
и DG
с данной окружностью. Тогда \cup AC_{1}=\cup AC
и \cup BE_{1}=\cup BE
.
Решение. Обозначим через C_{1}
и E_{1}
точки пересечения лучей DF
и DG
с данной окружностью. Поскольку окружность симметрична относительно диаметра AB
и
\angle AFC_{1}=\angle DFB=\angle AFC,
то точка C_{1}
симметрична точке C
относительно AB
. Поэтому \cup AC_{1}=\cup AC
. Аналогично \cup BE_{1}=\cup BE
. Следовательно,
\angle C_{1}DE_{1}=\frac{1}{2}\cup C_{1}E_{1}=\frac{1}{2}(180^{\circ}-60^{\circ}-20^{\circ})=50^{\circ}.