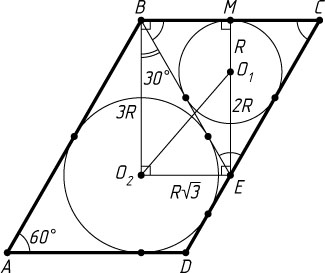
339. В параллелограмме ABCD
с углом A
, равным 60^{\circ}
, проведена биссектриса угла B
, пересекающая сторону CD
в точке E
. В треугольник ECB
вписана окружность радиуса R
. Другая окружность вписана в трапецию ABED
. Найдите расстояние между центрами этих окружностей.
Ответ. R\sqrt{7}
.
Указание. Треугольник с вершинами в точке E
и в центрах окружностей — прямоугольный.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей, вписанных соответственно в треугольник BCE
и в трапецию ABED
. Треугольник O_{1}EO_{2}
— прямоугольный, так как угол O_{1}EO_{2}
— прямой (угол между биссектрисами смежных углов). Треугольник BCE
— равносторонний
(\angle BEC=\angle ABE=\angle EBC=60^{\circ}),
O_{1}E=2R
, высота EM
равна 3R
. Поэтому
O_{2}B=EM=3R.
Тогда
EO_{2}=O_{2}B\tg\angle O_{2}BE=3R\tg30^{\circ}=R\sqrt{3}.
Следовательно,
O_{1}O_{2}=\sqrt{4R^{2}+3R^{2}}=R\sqrt{7}.