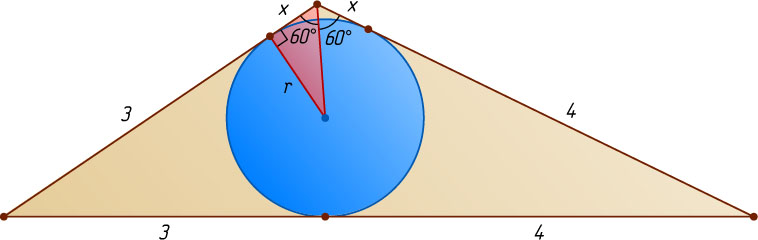
359. Окружность, вписанная в треугольник, точкой касания делит одну из сторон на отрезки, равные 3 и 4, а противолежащий этой стороне угол равен 120^{\circ}
. Найдите площадь треугольника.
Ответ. 4\sqrt{3}
.
Указание. Примените теорему косинусов.
Решение. Обозначим через x
расстояние от вершины угла в 120^{\circ}
до ближайшей точки касания и применим теорему косинусов. Получим уравнение x^{2}+7x-4=0
, из которого находим, что x=\frac{\sqrt{65}-7}{2}
.
Первый способ. Пусть p
— полупериметр треугольника, r
— радиус вписанной окружности, S
— площадь. Тогда
p=3+4+\frac{\sqrt{65}-7}{2}=\frac{\sqrt{65}+7}{2},~r=x\tg60^{\circ}=x\sqrt{3}=\frac{(\sqrt{65}-7)\sqrt{3}}{2}.
Следовательно,
S=pr=\frac{\sqrt{65}+7}{2}\cdot\frac{(\sqrt{65}-7)\sqrt{3}}{2}=4\sqrt{3}.
Второй способ.
S=\frac{1}{2}AB\cdot AC\sin120^{\circ}=\frac{1}{2}(x+3)(x+4)\sin120^{\circ}=
=\frac{1}{2}\left(\frac{\sqrt{65}-7}{2}+3\right)\left(\frac{\sqrt{65}-7}{2}+4\right)\cdot\frac{\sqrt{3}}{2}=
=\frac{1}{2}\cdot\frac{\sqrt{65}-1}{2}\cdot\frac{\sqrt{65}+1}{2}\cdot\frac{\sqrt{3}}{2}=\frac{1}{2}\cdot\frac{65-1}{4}\cdot\frac{\sqrt{3}}{2}=4\sqrt{3}.