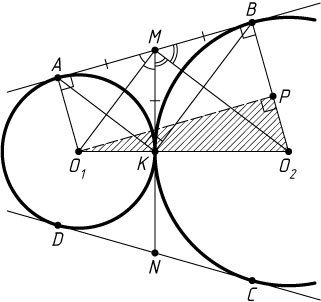
365. Окружности радиусов r
и R
(R\gt r)
касаются внешним образом в точке K
. К ним проведены две общие внешние касательные. Их точки касания с меньшей окружностью — A
и D
, с большей — B
и C
соответственно.
а) Найдите AB
и отрезок MN
общей внутренней касательной, заключённый между внешними касательными.
б) Докажите, что углы AKB
и O_{1}MO_{2}
— прямые (O_{1}
и O_{2}
— центры окружностей).
Ответ. 2\sqrt{rR}
.
Указание. Опустите перпендикуляр O_{1}P
из центра O_{1}
на O_{2}B
и рассмотрите полученный прямоугольный треугольник. Отрезки касательных, проведённых из одной точки к окружности, равны между собой.
Решение. а) Опустим перпендикуляр O_{1}P
из центра O_{1}
на O_{2}B
. Из прямоугольного треугольника O_{1}PO_{2}
находим, что
O_{1}O_{2}=r+R,~O_{2}P=R-r,~O_{1}P=\sqrt{O_{1}O_{2}^{2}-O_{2}P^{2}}=2\sqrt{rR}.
Поэтому AB=O_{1}P=2\sqrt{rR}
.
Поскольку MK=MB
и MK=MA
, то
NM=2MK=AB=2\sqrt{rR}.
б) Поскольку MO_{1}
и MO_{2}
— биссектрисы смежных углов AMK
и BMK
, то угол O_{1}MO_{2}
— прямой.
Поскольку MA=MK=MB
, то точка K
лежит на окружности с диаметром AB
. Поэтому \angle AKB=90^{\circ}
.