392. Докажите, что площадь треугольника можно выразить по формуле S=(p-a)r_{a}
, где r_{a}
— радиус вневписанной окружности, касающейся стороны, равной a
, p
— полупериметр треугольника.
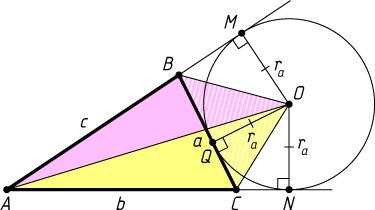
Решение. Первый способ. Пусть O
— центр окружности радиуса r_{a}
, касающейся стороны BC=a
треугольника ABC
в точке Q
, а продолжений сторон AB=c
и AC=b
— в точках M
и N
соответственно. Тогда
S_{\triangle ABC}=S_{\triangle AOB}+S_{\triangle AOC}-S_{\triangle BOC}=\frac{1}{2}AB\cdot OM+\frac{1}{2}AC\cdot ON-\frac{1}{2}BC\cdot OQ=
=\frac{1}{2}c\cdot r_{a}+\frac{1}{2}b\cdot r_{a}-\frac{1}{2}a\cdot r_{a}=\frac{c+b-a}{2}r_{a}=(p-a)r_{a}.
Второй способ. Пусть вписанная окружность с центром I
касается стороны AB=a
треугольника ABC
в точке P
, а вневписанная окружность с центром O
, касающаяся стороны BC
, касается продолжения стороны AB
в точке N
. Тогда AP=p-a
(см. задачу 219) и AQ=p
(см. задачу 1750).
Точки I
и O
лежат на одной прямой (см. задачу 1724), поэтому прямоугольные треугольники AIP
и AON
подобны. Следовательно,
\frac{r}{r_{a}}=\frac{AP}{AN}=\frac{p-a}{p}.
Следовательно (см. задачу 452),
S_{\triangle ABC}=pr=(p-a)r_{a}.
Примечание. См. также статью А.Блинкова и Ю.Блинкова «Вневписанная окружность», Квант, 2009, N2, с.34-37, 45.
