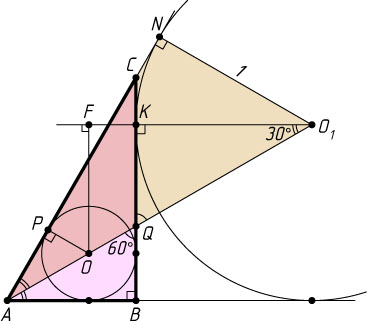
393. Площадь треугольника ABC
равна 2\sqrt{3}-3
, а угол BAC
равен 60^{\circ}
. Радиус окружности, касающейся стороны BC
и продолжения сторон AB
и AC
, равен 1. Найдите углы ABC
и ACB
данного треугольника.
Ответ. 90^{\circ}
, 30^{\circ}
.
Указание. Найдите радиус вписанной окружности и расстояние между центрами вписанной и данной окружностей.
Решение. Пусть O_{1}
— центр данной окружности, N
— её точка касания с прямой AC
, K
— со стороной BC
.
Из прямоугольного треугольника AO_{1}N
находим, что
AN=O_{1}N\ctg30^{\circ}=\sqrt{3}.
С другой стороны, AN
равно полупериметру p
треугольника ABC
(см. задачу 4805). Радиус вписанной окружности треугольника ABC
равен
\frac{S_{\triangle ABC}}{p}=\frac{2\sqrt{3}-3}{\sqrt{3}}=2-\sqrt{3}.
Если O
— центр этой окружности, а P
— точка касания со стороной AC
, то
O_{1}O=AO_{1}-AO=2O_{1}N-2OP=2(\sqrt{3}-1).
Пусть F
— основание перпендикуляра, опущенного из точки O
на продолжение отрезка O_{1}K
. Тогда
\cos\angle OO_{1}F=\frac{O_{1}F}{O_{1}O}=\frac{1+2-\sqrt{3}}{2(\sqrt{3}-1)}=\frac{\sqrt{3}}{2}.
Поэтому \angle OO_{1}F=30^{\circ}
. Если отрезки OO_{1}
и BC
пересекаются и точке Q
, то
\angle AQB=\angle O_{1}QK=60^{\circ}.
Следовательно,
\angle BCA=\angle AQB-\angle QAC=60^{\circ}-30^{\circ}=30^{\circ}.