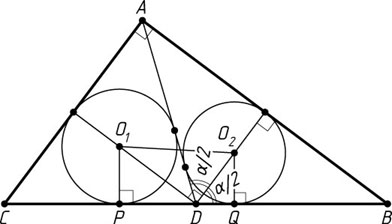
411. В прямоугольном треугольнике ABC
катеты AB
и AC
равны 4 и 3 соответственно. Точка D
делит гипотенузу BC
пополам. Найдите расстояние между центрами окружностей, вписанных в треугольники ADC
и ABD
.
Ответ. \frac{5\sqrt{13}}{12}
.
Указание. Если O_{1}
и O_{2}
— центры данных окружностей, то треугольник O_{1}DO_{2}
— прямоугольный.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей, вписанных в треугольники ADC
и ABD
соответственно, P
и Q
— их точки касания со стороной BC
. Обозначим \angle ADB=\alpha
.
Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы (см. задачу 1109), поэтому треугольника ADB
равнобедренный. Тогда
\sin\frac{\alpha}{2}=\frac{4}{5},~\cos\frac{\alpha}{2}=\frac{3}{5},
DQ=\frac{DB+AD+AB)}{2}-AB=\frac{1}{2}
(см. задачу 219). Аналогично находим, что DP=1
. Тогда
DO_{2}=\frac{DQ}{\cos\frac{\alpha}{2}}=\frac{5}{6},
DO_{1}=\frac{DP}{\cos\left(90^{\circ}-\frac{\alpha}{2}\right)}=\frac{DP}{\sin\frac{\alpha}{2}}=\frac{5}{4},
O_{1}O^{2}_{2}=DO^{2}_{1}+DO^{2}_{2}=\left(\frac{5}{4}\right)^{2}+\left(\frac{5}{6}\right)^{2}=\frac{25\cdot13}{144}.
Следовательно,
O_{1}O_{2}=\frac{5\sqrt{13}}{12}.