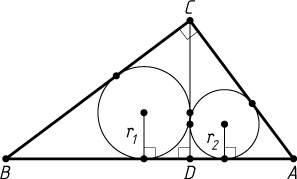
413. Прямоугольный треугольник ABC
разделён высотой CD
, проведённой к гипотенузе, на два треугольника: BCD
и ACD
. Радиусы окружностей, вписанных в эти треугольники, равны 4 и 3 соответственно. Найдите радиус окружности, вписанной в треугольник ABC
.
Ответ. 5.
Указание. Отношение радиусов окружностей, вписанных в подобные треугольники, равно коэффициенту подобия.
Решение. Пусть r
— искомый радиус, r_{1}
и r_{2}
— радиусы данных окружностей. Из подобия треугольников CBD
и ABC
находим, что \frac{r_{1}}{r}=\frac{BC}{AB}
, а из подобия треугольников ACD
и ABC
— \frac{r_{2}}{r}=\frac{AC}{AB}
. Возведём обе части этих равенств в квадрат и сложим почленно полученные равенства. Тогда
\frac{r^{2}_{1}}{r^{2}}+\frac{r^{2}_{2}}{r^{2}}=\frac{BC^{2}}{AB^{2}}+\frac{AC^{2}}{AB^{2}}=1,~r^{2}=r^{2}_{1}+r^{2}_{2}=16+9=25.
Следовательно, r=5
.