476. Во вписанном в окружность четырёхугольнике две противоположные стороны взаимно перпендикулярны, одна из них равна a
, а прилежащий к ней угол делится диагональю на части \alpha
и \beta
(угол \alpha
прилежит к данной стороне). Найдите диагонали четырёхугольника.
Ответ. \frac{a\sin(\alpha+\beta)}{\cos(2\alpha+\beta)}
; \frac{a\cos(\alpha+\beta)}{\cos(2\alpha+\beta)}
.
Указание. Радиус окружности, описанной около треугольника, равен стороне треугольника, делённой на удвоенный синус противолежащего угла.
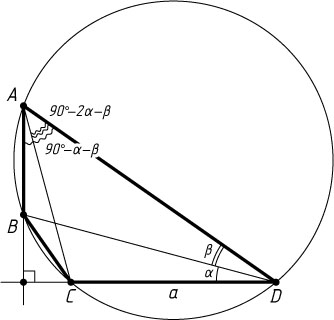
Решение. Пусть угол D
четырёхугольника ABCD
— острый,
CD\perp AB,~CD=a,~\angle CDB=\alpha,~\angle BDA=\beta,
R
— радиус окружности. Тогда
\angle BAD=90^{\circ}-\alpha-\beta,~\angle BAC=\alpha,~\angle CAD=90^{\circ}-2\alpha-\beta.
Поэтому
R=\frac{CD}{2\sin(90^{\circ}-2\alpha-\beta)}=\frac{a}{2\cos(2\alpha+\beta)},
AC=2R\sin(\alpha+\beta)=\frac{a\sin(\alpha+\beta)}{\cos(2\alpha+\beta)},
BD=2R\sin(90^{\circ}-\alpha-\beta)=\frac{a\cos(\alpha+\beta)}{\cos(2\alpha+\beta)}.
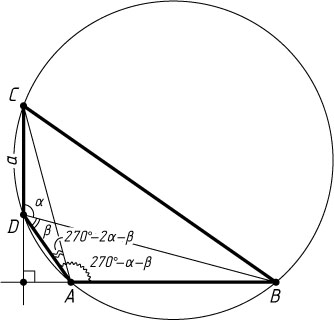
Если D
— тупой угол, то решение аналогично.