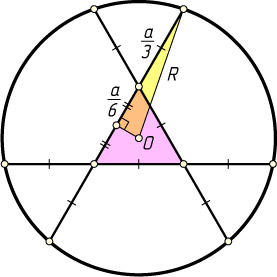
509. В окружности проведены три попарно пересекающиеся хорды. Каждая хорда разделена точками пересечения на три равные части. Найдите радиус окружности, если одна из хорд равна a
.
Ответ. \frac{a\sqrt{7}}{3\sqrt{3}}
.
Указание. Докажите, что все три хорды равны между собой.
Решение. Из теоремы о произведениях отрезков пересекающихся хорд следует, что все три хорды равны между собой. Поэтому точки пересечения хорд — вершины правильного треугольника со стороной \frac{a}{3}
. Поскольку равные хорды равноудалены от центра окружности, то центр O
этого треугольника совпадает с центром данной окружности. Расстояние от точки O
до каждой хорды равно \frac{a\sqrt{3}}{18}
. Пусть R
— искомый радиус. По теореме Пифагора находим, что
R^{2}=\left(\frac{a}{2}\right)^{2}+\left(\frac{a\sqrt{3}}{18}\right)^{2}=\frac{7a^{2}}{27}.
Следовательно,
R=\frac{a\sqrt{7}}{3\sqrt{3}}.