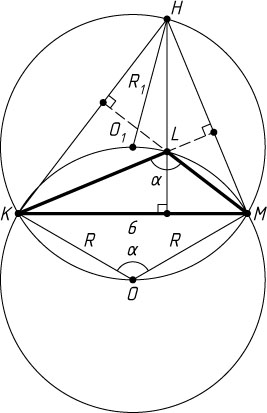
665. В треугольнике KLM
угол L
тупой, а сторона KM
равна 6. Найдите радиус описанной около треугольника KLM
окружности, если известно, что её центр лежит на окружности, проходящей через вершины K
, M
и точку пересечения высот треугольника KLM
.
Ответ. 2\sqrt{3}
.
Решение. Пусть H
— точка пересечения высот треугольника ABC
. Обозначим \angle KLM=\alpha
, R
и R_{1}
— радиусы окружностей, описанных около треугольников KLM
и KHM
соответственно. Тогда \angle KHM=180^{\circ}-\alpha
.
По теореме синусов
R=\frac{KM}{2\sin\angle KLM}=\frac{KM}{2\sin\alpha},~
R_{1}=\frac{KM}{2\sin\angle KHM}=\frac{KM}{2\sin(180^{\circ}-\alpha)}=\frac{KM}{2\sin\alpha}=R,
Поскольку центр O
описанной окружности треугольника KLM
, лежит на описанной окружности треугольника KHM
, четырёхугольник OKHM
вписанный, поэтому
\angle KOM=180^{\circ}-\angle KHM=\alpha.
Дуги KOM
и KLM
равны как дуги равных окружностей с общей хордой KM
, а KOM
— центральный угол, поэтому
\angle KOM=\smile KLM=2(180^{\circ}-\angle KLM)=360^{\circ}-2\alpha,
значит, \alpha=360^{\circ}-2\alpha
. Отсюда находим, что \alpha=120^{\circ}
. Следовательно,
R=\frac{KM}{2\sin120^{\circ}}=\frac{6}{\sqrt{3}}=2\sqrt{3}.