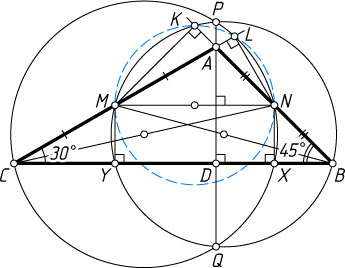
671. В треугольнике ABC
угол B
равен 45^{\circ}
, угол C
равен 30^{\circ}
. На медианах BM
и CN
как на диаметрах построены окружности, пересекающиеся в точках P
и Q
. Хорда PQ
пересекает сторону BC
в точке D
. Найдите отношение отрезков BD
и DC
.
Ответ. \frac{1}{\sqrt{3}}
.
Указание. Примените теорему об отрезках пересекающихся хорд.
Решение. Первый способ. Пусть окружности, построенные как на диаметрах на медианах BM
и CN
, пересекают сторону BC
в точках X
и Y
соответственно. Тогда X
и Y
— проекции точек N
и M
на сторону BC
.
Из прямоугольных треугольников BXN
и CYM
находим, что
YC=MY\sqrt{3}=NX\sqrt{3}.
По теореме о равенстве произведений отрезков пересекающихся хорд
BD\cdot DY=PD\cdot DQ=DX\cdot DC.
Поэтому
(BX+XD)DY=XD(DY+YC),~BX\cdot DY=DX\cdot CY,
или
BX\cdot DY=DX\cdot BX\sqrt{3}.
Следовательно,
DY=DX\sqrt{3},~~\frac{BD}{DC}=\frac{BX+DX}{DY+CY}=\frac{DX+BX}{DX\sqrt{3}+BX\sqrt{3}}=\frac{1}{\sqrt{3}}.
Второй способ. Линия центров указанных окружностей перпендикулярна их общей хорде PQ
и параллельна основаниям BC
и MN
трапеции BNMC
, значит, PQ\perp MN
. Кроме того, прямая PQ
— радикальная ось этих окружностей.
Пусть окружность с диаметром BM
пересекает прямую AB
в точке K
, а окружность с диаметром CN
пересекает прямую AC
в точке L
. Тогда MK
и NL
— высоты треугольника MAN
. Из точек K
и L
отрезок MN
виден под прямым углом, значит, эти точки лежат на окружности с диаметром MN
. Поэтому AK\cdot AN=AL\cdot AM
, а так как MN
— средняя линия треугольника ABC
, то AN=\frac{1}{2}AB
и AM=\frac{1}{2}AC
, значит, AK\cdot AB=AL\cdot AC
, т. е. степени точки A
относительно окружностей с диаметрами BM
и CN
равны. Значит, точка A
лежит на радикальной оси этих окружностей, т. е. на прямой PQ
, а AD
— высота треугольника ABC
. Тогда
BD=AD,~DC=AD\ctg30^{\circ}=AD\sqrt{3}.
Следовательно,
\frac{BD}{DC}=\frac{AD}{AD\sqrt{3}}=\frac{1}{\sqrt{3}}.