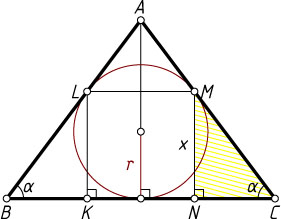
689. В равнобедренный треугольник ABC
вписан квадрат так, что две его вершины лежат на основании BC
, а две другие — на боковых сторонах треугольника. Сторона квадрата относится к радиусу круга, вписанного в треугольник, как 8:5
. Найдите углы треугольника.
Ответ. 2\arctg\frac{1}{2}
, 2\arctg\frac{1}{2}
, 180^{\circ}-4\arctg\frac{1}{2}
.
Указание. Выразите радиус вписанной окружности через сторону квадрата и тангенс половины угла при основании.
Решение. Пусть вершины K
и N
квадрата KLMN
принадлежат основанию BC
треугольника ABC
. Обозначим сторону квадрата через x
, радиус окружности, вписанной в треугольник ABC
— через r
, угол при основании треугольника — \alpha
. Тогда, если точка N
лежит между K
и C
, то
NC=\frac{MN}{\tg\alpha}=\frac{x}{\tg\alpha},~BC=BK+KN+NC=\frac{2x}{\tg\alpha}+x,
r=\frac{1}{2}BC\tg\frac{\alpha}{2}=\frac{1}{2}\left(\frac{2x}{\tg\alpha}+x\right)\tg\frac{\alpha}{2}=\frac{x}{2}\left(1-\tg^{2}\frac{\alpha}{2}+\tg\frac{\alpha}{2}\right),
или
1-\tg^{2}\frac{\alpha}{2}+\tg\frac{\alpha}{2}=\frac{2r}{x}=\frac{5}{4}.
Из полученного уравнения находим, что \tg\frac{\alpha}{2}=\frac{1}{2}
.