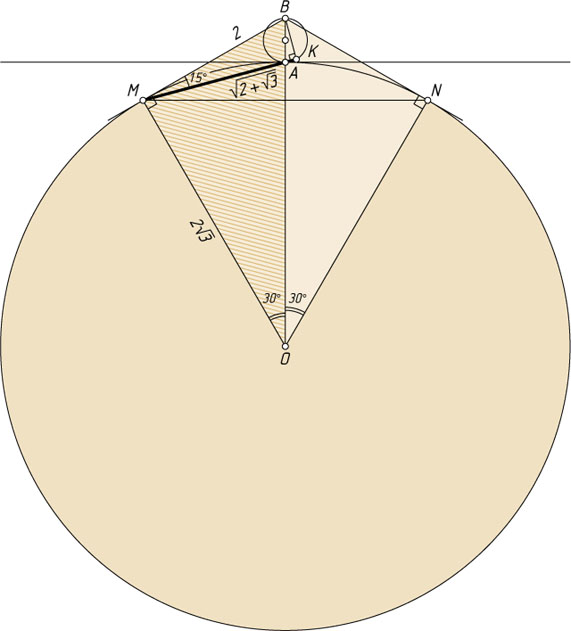
725. Две окружности разных радиусов касаются в точке A
одной и той же прямой и расположены по разные стороны от неё. Отрезок AB
— диаметр меньшей окружности. Из точки B
проведены две прямые, касающиеся большей окружности в точках M
и N
. Прямая, проходящая через точки M
и A
, пересекают меньшую окружность в точке K
. Известно, что MK=\sqrt{2+\sqrt{3}}
, а угол BMA
равен 15^{\circ}
. Найдите площадь фигуры, ограниченной отрезками касательных BM
, BN
и той дугой MN
большей окружности, которая не содержит точку A
.
Ответ. 4\sqrt{3}+10\pi
.
Указание. Примените теорему об угле между касательной и хордой.
Решение. Пусть O
— центр большей окружности. Угол между касательной BM
и хордой AM
равен 15^{\circ}
. Поэтому
\angle AOM=2\cdot15^{\circ}=30^{\circ},~\angle MKB=\angle AKB=90^{\circ}
(вписанный угол, опирающийся на диаметр AB
меньшей окружности). Тогда
BM=\frac{MK}{\cos\angle BMK}=\frac{MK}{\cos15^{\circ}}=
=\frac{\sqrt{2+\sqrt{3}}}{\frac{\sqrt{2+\sqrt{3}}}{2}}=2,
OM=BM\cos30^{\circ}=2\sqrt{3}.
Если S
— искомая площадь, то S=2S_{\triangle BMO}+S_{1}
, где S_{1}
— разность между площадью круга (\pi(2\sqrt{3})^{2}=12\pi
) и площадью сектора MON
с углом 60^{\circ}
между радиусами (12\pi-\frac{12\pi}{6}=10\pi
). Следовательно, искомая площадь равна
2BM\cdot\frac{1}{2}OM+10\pi=4\sqrt{3}+10\pi.