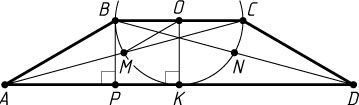
741. Окружность, построенная на основании BC
трапеции ABCD
как на диаметре, проходит через середины диагоналей AC
и BD
трапеции и касается основания AD
. Найдите углы трапеции.
Ответ. 30^{\circ}
, 30^{\circ}
, 150^{\circ}
, 150^{\circ}
.
Указание. Если O
— центр окружности, а M
— середина диагонали AC
, то OM
— средняя линия треугольника ABC
.
Решение. Обозначим через R
радиус окружности. Пусть O
— её центр, M
и N
— середины диагоналей AC
и BD
соответственно, K
— точка касания окружности с основанием AD
, P
— проекция вершины B
на основание AD
. Тогда OM=R
— средняя линия треугольника ABC
. Поэтому
AB=2OM=2R,~BP=OK=R.
Из прямоугольного треугольника BAP
находим, что \angle BAP=30^{\circ}
. Аналогично \angle CDA=30^{\circ}
.