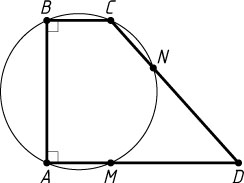
743. Окружность радиуса R
, проведённая через вершины A
, B
и C
прямоугольной трапеции ABCD
(\angle A=\angle B=90^{\circ}
) пересекает отрезки AD
и CD
соответственно в точках M
и N
, причём AM:AD=CN:CD=1:3
. Найдите площадь трапеции.
Ответ. \frac{4\sqrt{5}R^{2}}{3}
.
Указание. Докажите, что AD=DC
.
Решение. Поскольку DC\cdot DN=DA\cdot DM
, то \frac{2}{3}DC^{2}=\frac{2}{3}DA^{2}
. Поэтому DC=DA
.
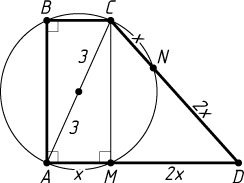
Обозначим AM=x
. Тогда MD=2x
, CD=AD=3x
. Поскольку точка M
лежит на окружности с диаметром AC
, то CM\perp AD
. По теореме Пифагора
CM^{2}=AC^{2}-AM^{2}=CD^{2}-DM^{2}.
Поэтому
4R^{2}-x^{2}=9x^{2}-4x^{2}.
Отсюда находим, что x=\frac{R\sqrt{2}}{\sqrt{3}}
. Тогда
CM^{2}=4R^{2}-\frac{2}{3}R^{2}=\frac{10}{3}10R^{2}.
Следовательно,
S_{ABCD}=\frac{1}{2}(AD+BC)CM=2x\cdot CM=
=\frac{2R\sqrt{2}\cdot R\sqrt{10}}{\sqrt{3}\cdot\sqrt{3}}=\frac{4R^{2}\sqrt{5}}{3}.