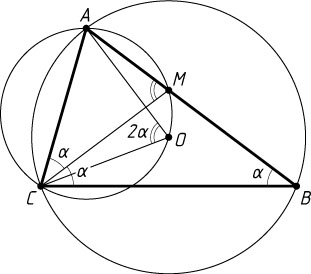
760. В треугольнике ABC
угол ABC
равен \alpha
, угол BCA
равен 2\alpha
. Окружность, проходящая через точки A
, C
и центр описанной около треугольника ABC
окружности, пересекает сторону AB
в точке M
. Найдите отношение AM
к AB
.
Ответ. \frac{1}{4\cos^{2}\alpha}
.
Указание. Докажите, что CM
— биссектриса треугольника ABC
.
Решение. Пусть O
— центр окружности, описанной около треугольника ABC
. Тогда по теореме об измерении вписанного угла и по теореме о внешнем угле треугольника
\angle AOC=2\angle ABC=2\alpha,~\angle AMC=\angle AOC=2\alpha,
\angle MCB=\angle AMC-\angle MBC=2\alpha-\alpha=\alpha,
а так как \angle ACB=2\alpha
, то CM
— биссектриса треугольника ACB
. Следовательно,
\frac{AM}{MB}=\frac{AC}{BC}=\frac{\sin\alpha}{\sin(180^{\circ}-3\alpha)}=\frac{\sin\alpha}{\sin3\alpha}.
Поэтому
\frac{AM}{AB}=\frac{\sin\alpha}{\sin\alpha+\sin3\alpha}=\frac{\sin\alpha}{2\sin2\alpha\cos\alpha}=\frac{\sin\alpha}{4\sin\alpha\cos^{2}\alpha}=\frac{1}{4\cos^{2}\alpha}.