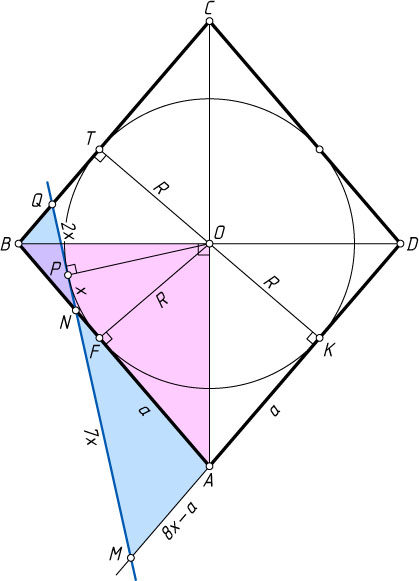
765. В ромб ABCD
вписана окружность. Прямая, касающаяся этой окружности в точке P
, пересекает стороны AB
, BC
и продолжение стороны AD
соответственно в точках N
, Q
и M
, причём MN:NP:PQ=7:1:2
. Найдите углы ромба.
Ответ. 2\arctg\frac{6}{7}=\arcsin\frac{84}{85}
, 180^{\circ}-2\arctg\frac{6}{7}=180^{\circ}-\arcsin\frac{84}{85}
.
Указание. Обозначьте MN=7x
, NP=x
, PQ=2x
и, воспользовавшись подобием треугольников BQN
и AMN
, выразите через x
сторону ромба.
Решение. Пусть K
, F
и T
— точки касания окружности со сторонами AD
, AB
и BC
соответственно. Обозначим NM=7x
, NP=x
, PQ=2x
, R
— радиус окружности, O
— её центр, AF=AK=a
. Тогда
MK=MP=8x,~MA=MK-AK=8x-a.
Из подобия треугольников BQN
и AMN
находим, что
BQ=\frac{3}{7}MA=\frac{3}{7}(8x-a).
Тогда
BF=BT=BQ+QT=BQ+QP=\frac{3}{7}(8x-a)+2x=
=\frac{1}{7}(38x-3a),~BN=BF-NF=BF-NP=\frac{1}{7}(31x-3a).
Поскольку BN=\frac{3}{7}AN
, то
\frac{1}{7}(31x-3a)=\frac{3}{7}(a+x).
Из этого уравнения находим, что a=\frac{14x}{3}
. Тогда
AB=\frac{10}{3}BN=\frac{170x}{21}.
Из прямоугольного треугольника AOB
находим, что
OF^{2}=R^{2}=BF\cdot AF=16x^{2}.
Поэтому R=4x
. Следовательно,
\sin\angle ABC=\frac{2R}{AB}=\frac{84}{85}.