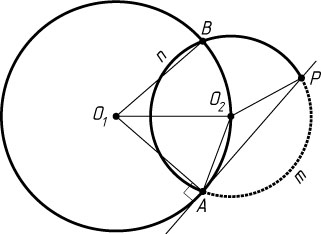
768. Первая из двух окружностей проходит через центр второй и пересекает её в точках A
и B
. Касательная к первой окружности, проходящая через точку A
, делит вторую окружность в отношении m:n
(m\lt n
). В каком отношении вторая окружность делит первую?
Ответ. \frac{n-m}{2m}
.
Указание. Примените теорему об угле между касательной и хордой.
Решение. Пусть O_{1}
и O_{2}
— центры соответственно первой и второй окружностей, P
— точка на второй окружности такая, что AP
— касательная к первой окружности. Тогда
\angle AO_{2}P=360^{\circ}\cdot\frac{m}{m+n},
\angle PAO_{2}=\frac{1}{2}(180^{\circ}-\angle AO_{2}P)=\frac{1}{2}\left(180^{\circ}-360^{\circ}\cdot\frac{m}{m+n}\right)=90^{\circ}\cdot\frac{n-m}{n+m}.
Поскольку \angle PAO_{2}
— угол между касательной и хордой, то
\angle AO_{1}O_{2}=2\angle PAO_{2}=180^{\circ}\cdot\frac{n-m}{n+m},
\angle AO_{1}B=2\angle AO_{1}O_{2}=360^{\circ}\cdot\frac{n-m}{n+m}.
Следовательно, в первой окружности
\smile AO_{2}B=360^{\circ}\cdot\frac{n-m}{n+m}.
Тогда дополнительная к ней дуга первой окружности равна 360^{\circ}\cdot\frac{2m}{n+m}
, а искомое отношение равно \frac{n-m}{2m}
.