788. Теорема о «трилистнике». Продолжение биссектрисы AD
треугольника ABC
пересекает описанную окружность в точке M
. Пусть I
— центр окружности, вписанной в треугольник ABC
. Докажите, что треугольники MBI
и MCI
— равнобедренные.
Указание. BI
— биссектриса угла ABC
.
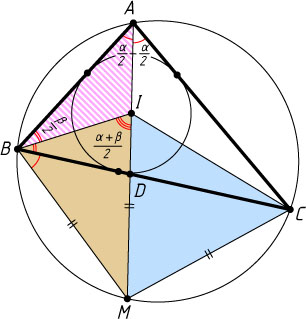
Решение. Первый способ. Обозначим \angle A=\alpha
, \angle B=\beta
.
Центр окружности, вписанной в треугольник, есть точка пересечения его биссектрис. Значит, BI
и AI
— биссектрисы углов ABC
и BAC
, а так как BIM
— внешний угол треугольника AIB
, то
\angle BIM=\angle ABI+\angle BAI=\frac{\alpha}{2}+\frac{\beta}{2}.
Вписанные углы MBC
и MAC
опираются на одну и ту же дугу, поэтому
\angle IBM=\angle IBC+\angle MBC=\angle IBD+\angle MAC=\frac{\beta}{2}+\frac{\alpha}{2}.
Следовательно, \angle BIM=\angle IBM
.
Аналогично \angle MCI=\angle MIC
.
Второй способ. Пусть биссектрисы углов при вершинах A
, B
и C
треугольника ABC
пересекают его описанную окружность в точках A_{1}
, B_{1}
и C_{1}
, а стороны B_{1}C_{1}
, A_{1}C_{1}
и A_{1}B_{1}
— в точках A_{2}
, B_{2}
и C_{2}
соответственно. Тогда A_{1}A_{2}
, B_{1}B_{2}
и C_{1}C_{2}
— высоты треугольника A_{1}B_{1}C_{1}
(см. задачу 33), а I
— ортоцентр этого треугольника. Поскольку B_{1}
и C_{1}
— середины меньших дуг AC
и AB
, лучи A_{1}B_{1}
и A_{1}C_{1}
— биссектрисы углов CA_{1}I
и BA_{1}I
. Тогда высоты A_{1}C_{2}
и A_{1}B_{2}
треугольников IA_{1}C
и IA_{1}B
являются биссектрисами. Значит, эти треугольники равнобедренные. Следовательно, A_{1}C=A_{1}I=A_{1}B
.
Примечание. 1. Верно и обратное утверждение: если биссектриса угла A
пересекает описанную окружность треугольника ABC
в точке M
и при этом для точки I
, лежащей на отрезке AM
, верны равенства MB=MA=MX
, то I
— центр вписанной окружности треугольника ABC
.
Доказательство. Достаточно доказать, что \angle ABI=\angle CBI
. По теореме о внешнем угле треугольника
\angle BIM=\angle ABI+\angle BAI=\angle ABI+\frac{1}{2}\angle BAC.
По теореме о вписанных углах
\angle CBM=\angle CAM=\frac{1}{2}\angle BAC,
поэтому
\angle MBI=\angle CBI+\angle CBM=\angle CBI+\frac{1}{2}\angle BAC.
Из равнобедренного треугольника MBI
получаем, что
\angle MBI=\angle BIM,~\mbox{или}~\angle CBI+\frac{1}{2}\angle BAC=\angle ABI+\frac{1}{2}\angle BAC,
откуда \angle ABI=\angle CBI
.
2. Пусть I_{a}
— центр вневписанной окружности треугольника ABC
, касающейся стороны BC
. Тогда по теореме Мансиона (см. задачу 57) точка M
— середина отрезка II_{a}
, поэтому MI_{a}=MI=MB=MC
.
3. Пусть P
— середина дуги ABC
описанной окружности треугольника ABC
, I_{c}
— центр вневписанной окружности треугольника ABC
, касающейся стороны AB
. Тогда PA=PC=PI_{c}
, т. е. P
— центр описанной окружности треугольника ACI_{c}
.
Доказательство. Поскольку P
— середина дуги ABC
, то PA=PB
. Осталось доказать, что PA=PI_{c}
.
Пусть I
— центр вписанной окружности треугольника ABC
, W
— точка пересечения биссектрисы угла ACB
с описанной окружностью этого треугольника. Тогда W
— середина отрезка II_{c}
, а AW
— медиана прямоугольного треугольника IAI_{c}
, проведённая из вершины прямого угла.
Обозначим \angle A=\alpha
, \angle B=\beta
, \angle C=\gamma
. Пусть K
— точка пересечения луча PW
с отрезком AI_{c}
. Тогда
\angle I_{c}WK=\angle CWP=\angle CAP=\angle CAB+\angle BAP=\frac{1}{2}(180^{\circ}-\angle ABC)=
=\frac{1}{2}(180^{\circ}-\angle ABC)=90^{\circ}-\frac{\beta}{2}=\frac{\alpha}{2}+\frac{\gamma}{2},
а по теореме о внешнем угле треугольника
\angle AWI_{c}=2\angle IAW=2\left(\frac{\alpha}{2}+\frac{\gamma}{2}\right)=\alpha+\gamma=2\angle I_{c}WK,
т. е. WK
— биссектриса, а значит, серединный перпендикуляр к основанию AI_{c}
равнобедренного треугольника AWI_{c}
. Точка P
лежит на этом серединном перпендикуляре, следовательно, PA=PI_{c}
. Что и требовалось доказать.
4. Из равенства MB=MI=MC
и задачи 6107 следует, что MI^{2}=MB^{2}=MC^{2}=MA\cdot MD
.
