811. Дан остроугольный треугольник ABC
. Для произвольной прямой l
обозначим через l_{a}
, l_{b}
, l_{c}
прямые, симметричные l
относительно сторон треугольника, а через O
— центр вписанной окружности треугольника, образованного этими прямыми. Найдите геометрическое место точек O
.
Ответ. Описанная окружность треугольника ABC
.
Решение. Пусть прямая l
пересекает прямые AB
, AC
и BC
в точках K
, M
и N
соответственно, а прямые l_{a}
, l_{b}
и l_{c}
симметричны прямой l
относительно прямых соответственно BC
, AC
и AB
. Пусть прямые l_{a}
и l_{b}
пересекаются в точке C_{1}
, прямые l_{a}
и l_{c}
— в точке B_{1}
, прямые l_{b}
и l_{c}
— в точке A_{1}
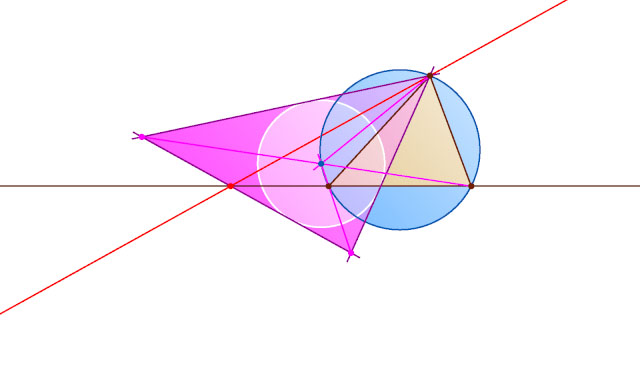
. Рассмотрим случай, изображённый на рис. 1.
Лучи KB
и NB
— биссектрисы внутренних углов треугольника KB_{1}N
, значит, луч BB_{1}
— биссектриса внутреннего угла при вершине B_{1}
этого треугольника (биссектрисы треугольника пересекаются в одной точке).
Луч KB
— биссектриса внутреннего угла при вершине K
треугольника KA_{1}M
, луч MA
— биссектриса внешнего угла при вершине M
этого треугольника, значит, луч AA_{1}
— биссектриса внешнего угла при вершине A_{1}
треугольника KA_{1}M
(биссектрисы двух внешних и третьего внутреннего углов треугольника пересекаются в одной точке — центре вневписанной окружности треугольника).
Аналогично докажем, что луч C_{1}C
— биссектриса внутреннего угла при вершине C_{1}
треугольника MC_{1}N
.
Биссектрисы вертикальных углов лежат на одной прямой, поэтому биссектрисы треугольника A_{1}B_{1}C_{1}
лежат на прямых AA_{1}
, BB_{1}
и CC_{1}
. Следовательно, эти прямые пересекаются в одной точке — центре O
вписанной окружности треугольника A_{1}B_{1}C_{1}
.
По теореме о внешнем угле треугольника
\angle ABC=\angle BNK+\angle BKN=90^{\circ}-\angle BB_{1}K,~
\angle AOC=\angle OA_{1}C_{1}+\angle OC_{1}A_{1}=90^{\circ}-\angle OB_{1}C_{1}=90^{\circ}-\angle BB_{1}K=\angle ABC.
Из точек O
и B
, лежащих по одну сторону от прямой AC
, отрезок AC
виден под одним и тем же углом, значит, точки A
, O
, B
и C
лежат на одной окружности — описанной окружности треугольника ABC
.
Аналогично для любого другого положения прямой l
. Возможно, что вместо рассматриваемых биссектрис внутренних (внешних) углов треугольников KB_{1}N
, KA_{1}M
и MC_{1}N
будут рассмотрены биссектрисы внешних (внутренних) углов этих треугольников.
Таким образом, доказано, что для любой прямой l
центр вписанной окружности соответствующего треугольника A_{1}B_{1}C_{1}
лежит на описанной окружности треугольника ABC
.
Докажем теперь, что для каждой точки описанной окружности треугольника ABC
найдётся прямая l
, для которой эта точка — центр вписанной окружности треугольника, построенного указанным в условии способом. Окажется, что в качестве этой прямой можно взять прямую, проходящую через вершину треугольника ABC
.
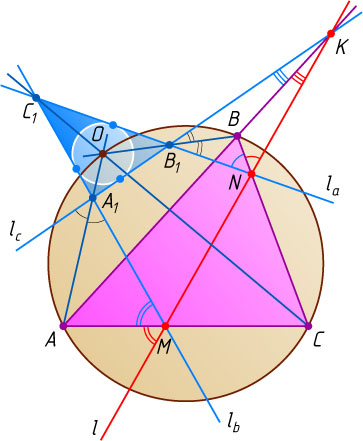
Пусть l
— произвольная прямая, проходящая через вершину B
(рис. 2), A_{1}BC_{1}
— соответствующий этой прямой треугольник, образованный прямыми l_{a}
, l_{b}
и l_{c}
(в этом случае B_{1}
— это точка B
), O
— центр вписанной окружности треугольника A_{1}BC_{1}
(точка O
лежит на описанной окружности треугольника ABC
).
Пусть l'
— другая прямая, проходящая через точку B
, \varphi
— угол между прямыми l
и l'
, A_{1}'BC_{1}'
— соответствующий прямой l'
треугольник, образованный прямыми l_{a}'
, l_{b}'
и l_{c}'
, O'
— центр его вписанной окружности. Докажем, что \angle OBO'=\varphi
. Действительно, при повороте на угол \varphi
вокруг точки B
прямая l
переходит в прямую l'
, прямая BA_{1}
— в прямую BA_{1}'
, а прямая BC_{1}
— в прямую BC_{1}'
, значит, \angle A_{1}BA_{1}'=\varphi
и \angle C_{1}BC_{1}'=\varphi
, а так как по доказанному BO
и BO'
— биссектрисы углов A_{1}BC_{1}
и A_{1}'BC_{1}'
, то угол между этими биссектрисами также равен \varphi
.
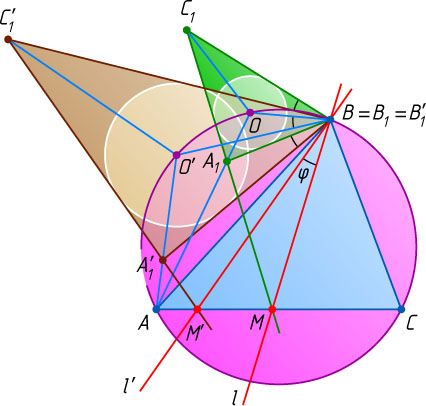
Таким образом, поворачивая прямую l
вокруг точки B
на угол \varphi
от 0^{\circ}
до 180^{\circ}
, мы также повернём и прямую BO
на этот же угол. Следовательно, мы можем получить всевозможные положения точки O
на описанной окружности треугольника ABC
(рис. 3).