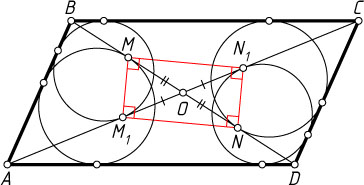
812. Каждая диагональ разбивает параллелограмм, не являющийся ромбом, на два треугольника. В каждый из этих четырёх треугольников вписана окружность. Докажите, что точки касания этих окружностей с диагоналями являются вершинами прямоугольника.
Решение. Пусть ABCD
— параллелограмм, в котором AB\lt BC
, M
и N
— точки касания с диагональю BD
вписанных окружностей равных треугольников ABD
и CDB
соответственно, M_{1}
и N_{1}
— точки касания с диагональю AC
вписанных окружностей равных треугольников ABC
и CDA
соответственно, O
— точка пересечения диагоналей параллелограмма.
Точка O
— центр симметрии параллелограмма, поэтому OM=ON
и OM_{1}=ON_{1}
, значит, MM_{1}NN_{1}
— параллелограмм.
Докажем, что MN=M_{1}N_{1}
. Действительно, для вписанной окружности треугольника ABD
известно, что BM=\frac{AB+BD-AD}{2}
(см. 219), а так как DN=BM
, то
MN=BD-2BM=BD-(AB+BD-AD)=AD-AB.
Аналогично, M_{1}N_{1}=AD-AB
. Что и требовалось доказать.
Таким образом, диагонали параллелограмма MM_{1}NN_{1}
равны, следовательно, это прямоугольник.