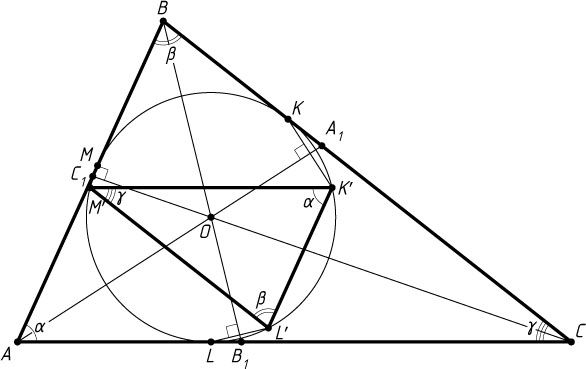
819. Рассмотрим три точки, каждая из которых симметрична точке касания окружности, вписанной в треугольник, относительно биссектрисы противолежащего этой стороне угла. Докажите, что эти три точки служат вершинами треугольника, подобного данному.
Решение. Пусть K
, L
и M
— точки касания окружности с центром O
, вписанной в треугольник ABC
, со сторонами BC
, AC
и AB
соответственно, AA_{1}
, BB_{1}
и CC_{1}
— биссектрисы треугольника ABC
, \alpha
, \beta
и \gamma
— углы треугольника при вершинах соответственно A
, B
и C
; K'
, L'
и M'
— точки, симметричные точкам K
, L
и M
относительно биссектрис AA_{1}
, BB_{1}
и CC_{1}
соответственно.
Тогда
\angle MOK=180^{\circ}-\beta,~
\angle MOM'=2\angle MOC_{1}=2(90^{\circ}-\angle OC_{1}M)=2\left(90^{\circ}-\beta-\frac{\gamma}{2}\right),~
\angle KOK'=2\angle KOA_{1}=2(90^{\circ}-\angle OA_{1}K)=2\left(90^{\circ}-\gamma-\frac{\alpha}{2}\right).
\angle K'OM'=\angle MOK-\angle MOM'+\angle KPK'=180^{\circ}-\beta-2\left(90^{\circ}-\beta-\frac{\gamma}{2}\right)+2\left(90^{\circ}-\gamma-\frac{\alpha}{2}\right)=
=180^{\circ}+\beta-\gamma-\alpha=(180^{\circ}-\gamma-\alpha)+\beta=\beta+\beta=2\beta.
Вписанный угол K'L'M'
равен половине центрального угла K'OM'
, т. е. \angle K'L'M'=\frac{1}{2}\cdot2\beta=\beta
. Аналогично \angle L'M'K'=\gamma
. Следовательно, треугольник K'L'M'
подобен треугольнику ABC
.