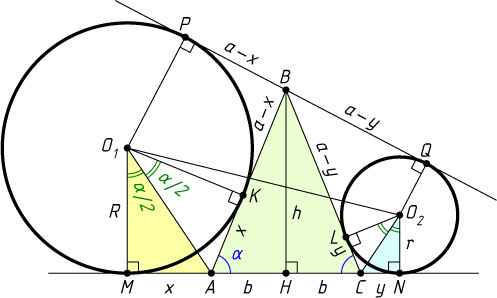
831. Даны две непересекающиеся окружности, к которым проведены две общие внешние касательные. Рассмотрим равнобедренный треугольник, основание которого лежит на одной касательной, противоположная вершина — на другой, а каждая из боковых сторон касается одной из данных окружностей. Докажите, что высота треугольника равна сумме радиусов окружностей.
Указание. Используя равенство отрезков касательных, проведённых из одной точки к окружности, выразите сумму радиусов данных окружностей через стороны данного треугольника и угол при его основании.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей, R
и r
— их радиусы (R\gt r
, AC
— основание данного треугольника ABC
, расположенное на общей касательной MN
(M
и N
— точки касания), PQ
— вторая общая касательная (P
и Q
— точки касания), K
— точка касания первой окружности со стороной AB
, L
— второй окружности со стороной BC
. Обозначим
AB=BC=a,~AC=2b,~\angle BAC=\angle BCA=\alpha,~AM=AK=x,~CN=CL=y,
h
— высота треугольника ABC
, проведённая из вершины B
.
Поскольку
PQ=MN,~PQ=PB+BQ=BK+BL=2a-x-y,
MN=MA+AC+CN=x+y+2b,
то 2a-x-y=x+y+2b
. Поэтому x+y=a-b
.
Из прямоугольных треугольников MAO_{1}
и NCO_{2}
находим, что
R=x\ctg\frac{\alpha}{2},~r=y\ctg\frac{\alpha}{2}.
Следовательно,
R+r=(x+y)\ctg\frac{\alpha}{2}=\frac{(a-b)(1+\cos\alpha)}{\sin\alpha}=
=\frac{(a-b)\left(1+\frac{b}{a}\right)}{\frac{h}{a}}=\frac{a^{2}-b^{2}}{h}=\frac{h^{2}}{h}=h.