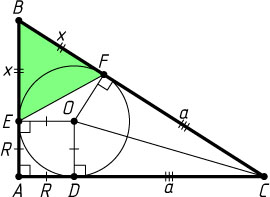
866. В треугольник ABC
вписана окружность радиуса R
, касающаяся стороны AC
в точке D
, стороны AB
в точке E
и стороны BC
в точке F
. Известно, что AD=R
, DC=a
. Найдите площадь треугольника BEF
.
Ответ. \frac{R^{2}(R+a)^{3}}{2(a-R)(a^{2}+R^{2})}
.
Указание. Треугольник ABC
— прямоугольный.
Решение. Пусть O
— центр окружности. Поскольку AE=AD=OD=OE=R
и OD\perp AD
, то AEOD
— квадрат. Поэтому треугольник ABC
— прямоугольный, \angle A=90^{\circ}
.
Обозначим BE=BF=x
. По теореме Пифагора
(x+R)^{2}+(R+a)^{2}=(x+a)^{2}.
Из полученного уравнения находим, что x=\frac{R(R+a)}{a-R}
.
Из прямоугольного треугольника ODC
находим, что \tg\frac{1}{2}\angle C=\frac{OD}{DC}=\frac{R}{a}
. Тогда
\sin\angle B=\cos\angle C=\frac{1-\left(\frac{R}{a}\right)^{2}}{1+\left(\frac{R}{a}\right)^{2}}=\frac{a^{2}-R^{2}}{a^{2}+R^{2}}.
Следовательно,
S_{\triangle BEF}=\frac{1}{2}BE\cdot BF\sin\angle B=\frac{1}{2}R^{2}\frac{(R+a)^{2}(a^{2}-R^{2})}{(a-R)^{2}(a^{2}+R^{2})}=\frac{R^{2}(R+a)^{3}}{2(a-R)(a^{2}+R^{2})}.