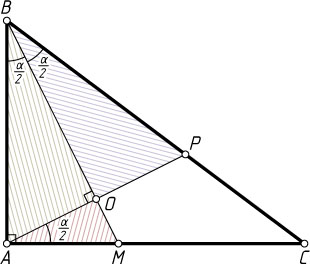
906. В треугольнике ABC
на стороне BC
взята точка P
, а на стороне AC
взята точка M
. Отрезки AP
и BM
пересекаются в точке O
. Известно, что треугольники BOP
, AOM
и BOA
подобны, BM=1
, косинус угла ABC
равен 0,6. Найдите площадь треугольника ABC
.
Ответ. \frac{8}{15}
.
Указание. Докажите, что треугольник ABC
— прямоугольный.
Решение. Из подобия треугольников BOP
, AOM
и BOA
следует равенство углов BOP
и BOA
, а так как это смежные углы, то
\angle BOP=\angle BOA=90^{\circ}.
Кроме того, \angle PBO=\angle ABO
. Поэтому BM
— биссектриса угла ABC
. Из равенства углов MAO
и ABO
следует, что \angle BAC=90^{\circ}
, т. е. треугольник ABC
— прямоугольный.
Пусть \angle ABC=\alpha
. Тогда
\angle ABM=\frac{\alpha}{2},~AB=BM\cos\frac{\alpha}{2}=1\cdot\sqrt{\frac{1+\cos\alpha}{2}}=
=\sqrt{\frac{1+\frac{3}{5}}{2}}=\frac{2}{\sqrt{5}}.
Из треугольника ABC
находим, что
AC=AB\tg\alpha=\frac{8}{3\sqrt{5}}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC=\frac{8}{15}.