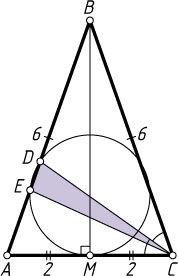
928. В равнобедренном треугольнике ABC
известно, что AC=4
, AB=BC=6
. Биссектриса угла C
пересекает сторону AB
в точке D
. Через точку D
проведена окружность, касающаяся стороны AC
в её середине и пересекающая отрезок AD
в точке E
. Найдите площадь треугольника DEC
.
Ответ. \frac{44\sqrt{2}}{45}
.
Указание. Примените теорему о касательной к секущей.
Решение. По свойству биссектрисы треугольника
\frac{AD}{DB}=\frac{AC}{BC}=\frac{2}{3}.
Поэтому AD=\frac{2}{5}AB=\frac{12}{5}
.
Пусть M
— середина AC
. Тогда
S_{\triangle ABC}=\frac{1}{2}AC\cdot BM=\frac{1}{2}AC\sqrt{AB^{2}-AM^{2}}=\frac{1}{2}\cdot4\sqrt{36-4}=2\sqrt{32}=8\sqrt{2}.
По теореме о касательной и секущей
AM^{2}=AD\cdot AE,~\mbox{или}~4=\frac{12}{5}\left(\frac{12}{5}-DE\right).
Отсюда находим, что DE=\frac{11}{15}
. Следовательно,
S_{\triangle DEC}=\frac{DE}{AB}S_{\triangle ABC}=\frac{44\sqrt{2}}{45}.