945. Окружность проходит через соседние вершины M
и N
прямоугольника MNPQ
. Длина касательной, проведённой из точки Q
к окружности, равна 1, PQ=2
. Найдите все возможные значения, которые может принимать площадь прямоугольника MNPQ
, если диаметр окружности равен \sqrt{5}
.
Ответ. \sqrt{5}\pm1
.
Решение. Пусть прямая MQ
вторично пересекает окружность в точке K
. Тогда \angle NMK=90^{\circ}
, поэтому NK
— диаметр окружности, NK=\sqrt{5}
. По теореме Пифагора
MK=\sqrt{NK^{2}-MN^{2}}=\sqrt{5-4}=1.
Пусть прямая, проведённая через вершину Q
, касается окружности в точке A
. По теореме о касательной и секущей то QM\cdot QK=QA^{2}
. Обозначим QM=x
.
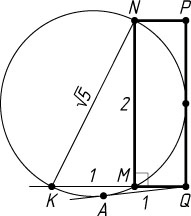
Если точка K
лежит на продолжении стороны QM
(рис. 1), то x(x+1)=1
, откуда x=\frac{\sqrt{5}-1}{2}
. Следовательно,
S_{MNPQ}=QM\cdot PQ=\frac{\sqrt{5}-1}{2}\cdot2=\sqrt{5}-1.
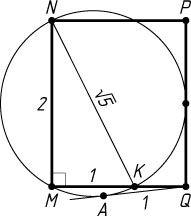
Если же точка K
лежит на отрезке QM
(рис. 2), то x(x-1)=1
, откуда x=\frac{\sqrt{5}+1}{2}
. Следовательно,
S_{MNPQ}=QM\cdot PQ=\frac{\sqrt{5}+1}{2}\cdot2=\sqrt{5}+1.