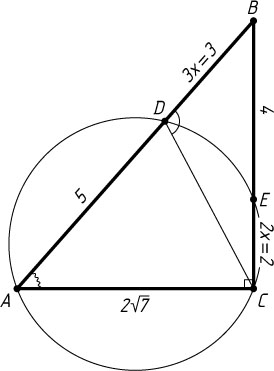
968. Окружность проходит через вершины A
и C
треугольника ABC
, пересекает сторону AB
в точке D
и сторону BC
в точке E
. Найдите угол CDB
, если AD=5
, AC=2\sqrt{7}
, BE=4
, BD:CE=3:2
.
Ответ. \arccos\left(-\frac{\sqrt{2}}{4}\right)
.
Указание. Произведение всей секущей на её внешнюю часть для данной точки и данной окружности постоянно.
Решение. Обозначим BD=3x
, CE=2x
.
Поскольку BD\cdot AB=BE\cdot BC
, то 3x\cdot(3x+5)=4(2x+4)
. Отсюда находим, что x=1
. Следовательно,
AB=AD+DB=8,~BC=BE+EC=6.
Поскольку AC^{2}+BC^{2}=28+36=64=AB^{2}
, то треугольник ABC
— прямоугольный, \cos\angle BAC=\frac{AC}{AB}=\frac{\sqrt{7}}{4}
.
По теореме косинусов из треугольника ADC
находим, что
DC^{2}=AD^{2}+AC^{2}-2AD\cdot AC\cos\angle DAC=
=25+28-2\cdot5\cdot2\sqrt{7}\cdot\frac{7}{4}=18.
По теореме косинусов из треугольника BDC
находим, что
\cos\angle BDC=\frac{BD^{2}+DC^{2}-BC^{2}}{2BD\cdot DC}=\frac{9+18-36}{2\cdot3\cdot3\sqrt{2}}=-\frac{\sqrt{2}}{4}.