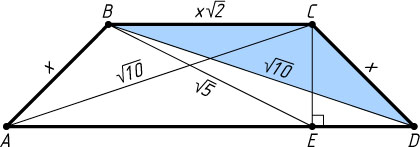
979. В равнобедренной трапеции ABCD
боковая сторона в \sqrt{2}
раз меньше основания BC
, CE
— высота. Найдите периметр трапеции, если BE=\sqrt{5}
, BD=\sqrt{10}
.
Ответ. 6+2\sqrt{2}
.
Указание. Обозначьте AB=CD=x
, выразите через x
косинус угла ADC
и примените теорему косинусов к треугольнику DBC
.
Решение. Обозначим AB=CD=x
. Тогда
BC=x\sqrt{2},~CE=\sqrt{BE^{2}-BC^{2}}=\sqrt{5-2x^{2}},
DE=\sqrt{CD^{2}-CE^{2}}=\sqrt{x^{2}-(5-2x^{2})}=\sqrt{3x^{2}-5},
\cos\angle ADC=\frac{DE}{CD}=\frac{\sqrt{3x^{2}-5}}{x}.
По теореме косинусов из треугольника DBC
находим, что
BD^{2}=BC^{2}+CD^{2}-2BC\cdot CD\cos\angle BCD=BC^{2}+CD^{2}+2BC\cdot CD\cos\angle ADC,
или
10=2x^{2}+x^{2}+2x\sqrt{3x^{2}-5}.
Из этого уравнения находим, что x^{2}=2
. Тогда
BC+AD=2AE=2\sqrt{AC^{2}-CE^{2}}=2\sqrt{5+2x^{2}}=2\cdot3=6.
Следовательно, периметр трапеции равен 6+2\sqrt{2}
.