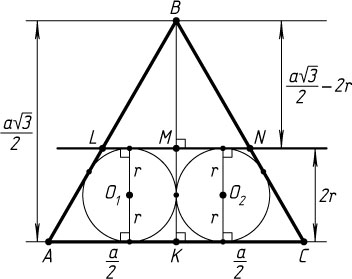
985. В правильном треугольнике ABC
, сторона которого равна a
, проведена высота BK
. В треугольники ABK
и BCK
вписано по окружности и к ним проведена общая внешняя касательная, отличная от стороны AC
. Найдите площадь треугольника, отсекаемого этой касательной от треугольника ABC
.
Ответ. \frac{a^{2}\sqrt{3}}{12}
.
Указание. Отсекаемый треугольник подобен треугольнику ABC
с коэффициентом \frac{1}{\sqrt{3}}
.
Решение. Стороны треугольника ABK
:
AB=a,~AK=\frac{a}{2},~BK=\frac{a\sqrt{3}}{2}.
Радиус окружности, вписанной в ABK
:
r=\frac{AK+BK-AB}{2}=\frac{a(\sqrt{3}-1)}{4}
(см. задачу 217). Пусть указанная касательная пересекает отрезки AB
, BK
, BC
в точках L
, M
, N
соответственно. Тогда
BM=BK-KM=\frac{a\sqrt{3}}{2}-2r=\frac{a\sqrt{3}}{2}-\frac{a(\sqrt{3}-1)}{2}=\frac{a}{2}.
Поэтому коэффициент подобия треугольников BLN
и BAC
равен
\frac{BM}{BK}=\frac{\frac{a}{2}}{\frac{a\sqrt{3}}{2}}=\frac{1}{\sqrt{3}}.
Следовательно,
S_{\triangle BLN}=\frac{1}{3}S_{\triangle BAC}=\frac{a^{2}\sqrt{3}}{12}.