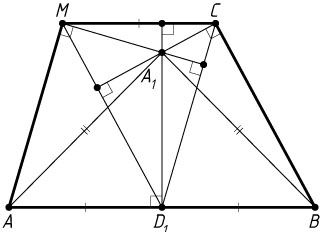
10390. В трапеции ABCD
основание AD
в два раза больше основания BC
. Внутри трапеции взяли точку M
так, что углы ABM
и DCM
прямые.
а) Докажите, что AM=DM
.
б) Найдите угол BAD
, если угол ADC
равен 55^{\circ}
, а расстояние от точки M
до прямой AD
равно стороне BC
.
Ответ. 80^{\circ}
.
Решение. а) Пусть N
— середина основания AD
. Поскольку AN=DN=\frac{1}{2}AD=BC
и BC\parallel AD
, четырёхугольники ABCN
и BCDN
— параллелограммы. Значит, CN\parallel AB
и BN\parallel CD
. Тогда высоты треугольника BNC
, проведённые из его вершин B
и C
, лежат на прямых BM
и CM
соответственно, а M
— ортоцентр треугольника BNC
. Следовательно, третья высота треугольника BNC
лежит на прямой MN
, т. е. MN\perp BC
.
Прямые AD
и BC
параллельны, поэтому MN\perp AD
. Тогда медиана MN
треугольника AMD
является его высотой, значит, этот треугольник равнобедренный. Следовательно, AM=DM
.
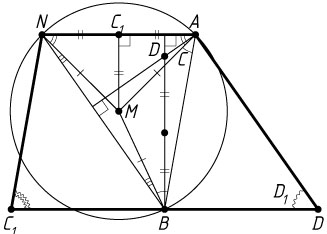
б) Пусть O
— центр окружности, описанной около треугольника BNC
, K
— середина стороны BC
. Тогда OK\perp BC
. Поскольку M
— ортоцентр треугольника отрезок OK
вдвое меньше MN
(см. задачу 1257), значит,
OK=\frac{1}{2}MN=\frac{1}{2}BC=BK.
Следовательно, \angle OCB=\angle OBC=45^{\circ}
.
Обозначим \angle OCN=\alpha
. Треугольники CON
и BON
равнобедренные, а противоположные углы CBN
и CDN
параллелограмма BCDN
равны, поэтому
\angle CNO=\alpha,~\angle BNO=\angle NBO=\angle NBC-\angle OBC=
=\angle CDN-\angle OBC=55^{\circ}-45^{\circ}=10^{\circ},
а так как сумма углов треугольника BCN
равна 180^{\circ}
, то
55^{\circ}+(45^{\circ}+\alpha)+(10^{\circ}+\alpha)=180^{\circ}.
Отсюда находим, что \alpha=35^{\circ}
, а так как ABCN
— параллелограмм, то
\angle BAD=\angle BAN=\angle BCN=45^{\circ}+\alpha=45^{\circ}+35^{\circ}=80^{\circ}.