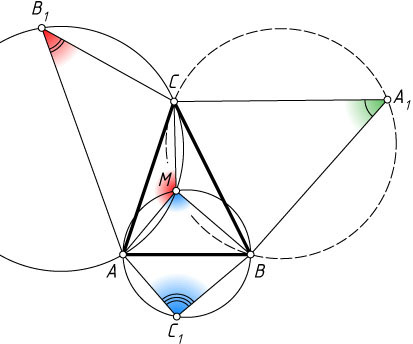
1080. На сторонах треугольника ABC
внешним образом построены треугольники ABC_{1}
, AB_{1}C
и A_{1}BC
, причём сумма их углов при вершинах A_{1}
, B_{1}
и C_{1}
равна 180^{\circ}
. Докажите, что описанные окружности построенных треугольников пересекаются в одной точке.
Указание. Докажите, что точка пересечения окружностей, описанных около двух из указанных треугольников, лежит на окружности, описанной около третьего. Рассмотрите все возможные случаи или воспользуйтесь ориентированными углами.
Решение. Обозначим через M
точку пересечения окружностей, описанных около треугольников ABC_{1}
и AB_{1}C
, отличную от A
, и докажем, что точка M
лежит на окружности, описанной около треугольника A_{1}BC
.
Пусть точка лежит внутри треугольника ABC
. Тогда
\angle BMC=360^{\circ}-\angle AMB-\angle AMC=
=360^{\circ}-(180^{\circ}-\angle AC_{1}B)-(180^{\circ}-\angle AB_{1}C)=\angle AC_{1}B+\angle AB_{1}C,
поэтому
\angle BMC+\angle BA_{1}C=\angle AC_{1}B+\angle AB_{1}C+\angle BA_{1}C=180^{\circ}.
Следовательно, точки B
, A_{1}
, M
, C
лежат на одной окружности, т. е. все три окружности проходят через точку M
.
Аналогично для остальных случаев.
Примечание. Утверждение останется верным, если сумма углов треугольников ABC_{1}
, AB_{1}C
и A_{1}BC
при вершинах A_{1}
, B_{1}
и C_{1}
равна 360^{\circ}
.
