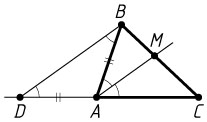
11357. В треугольнике ABC
на продолжении стороны AC
за вершину A
отложен отрезок AD
, равный стороне AB
. Прямая, проходящая через точку A
параллельно BD
, пересекает сторону BC
в точке M
.
а) Докажите, что AM
— биссектриса угла BAC
.
б) Найдите площадь трапеции AMBD
, если площадь треугольника ABC
равна 216, и известно отношение AC:AB=5:4
.
Ответ. 268\frac{4}{5}=268{,}8
.
Решение. а) Треугольник ABD
равнобедренный, поэтому \angle ABD=\angle ADB
. Из параллельности прямых AM
и BD
получаем, что \angle BAM=\angle ABD
(накрест лежащие углы при параллельных прямых AM
, BD
и секущей AB
) и \angle CAM=\angle ADB
(соответственные углы). Следовательно,
\angle CAM=\angle ADB=\angle ABD=\angle BAM,
т. е. AM
— биссектриса угла BAC
.
б) По теореме о пропорциональных отрезках и свойству биссектрисы треугольника (см. задачу 1509)
\frac{AC}{AD}=\frac{CM}{MB}=\frac{AC}{AB}=\frac{5}{4},
поэтому
S_{\triangle BAM}=\frac{BM}{BC}S_{\triangle ABC}=\frac{4}{9}\cdot216=96,~S_{\triangle ABD}=\frac{4}{5}S_{\triangle ABC}=\frac{4}{5}\cdot216=\frac{864}{5}
(см. задачу 3000). Следовательно,
S_{AMBD}=S_{\triangle BAM}+S_{\triangle ABD}=96+\frac{864}{5}=\frac{1344}{5}=268\frac{4}{5}=268{,}8.