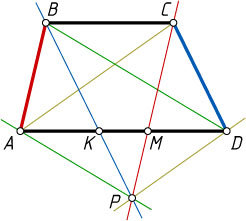
11397. В трапеции с основаниями AD
и BC
проведены четыре прямые: через вершину A
параллельно диагонали BD
, через вершину B
параллельно стороне CD
, через вершину C
параллельно стороне AB
, через вершину D
параллельно диагонали AC
. Оказалось, что эти прямые пересеклись в одной точке. Найдите отношение \frac{AD}{BC}
.
Ответ. \frac{1+\sqrt{5}}{2}
.
Решение. Положим BC=a
и AD=\lambda a
(\lambda\gt1
). Пусть прямые, проведённые через вершины A
и D
параллельно диагоналям BD
и AC
, пересекаются в точке P
, а прямые BP
и CP
пересекают основание AD
в точках K
и M
соответственно. Тогда
\lambda a=AD=AM+DK-KM=2a-KM,
откуда KM=(2-\lambda)a
(AM=DK=a
, так как ABCM
и BCDK
— параллелограммы).
Треугольник DMP
подобен треугольнику AMC
, а треугольник PKM
— треугольнику PBC
, поэтому
\frac{PM}{MC}=\frac{MD}{AM}=\frac{AD-AM}{AM}=\frac{\lambda a-a}{a}=\lambda-1,
\frac{PM}{MC}=\frac{PM}{PC-PM}=\frac{KM}{BC-KM}=\frac{(2-\lambda)a}{a-(2-\lambda)a}=\frac{2-\lambda}{\lambda-1}.
Значит, \frac{2-\lambda}{\lambda-1}=\lambda-1
. Из этого уравнения находим, что \lambda=\frac{1+\sqrt{5}}{2}
.