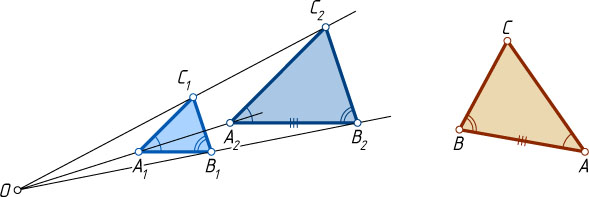
1289. Признак подобия треугольников по двум углам. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Указание. Пусть ABC
и A_{1}B_{1}C_{1}
— треугольники, у которых \angle A=\angle A_{1}
и \angle B=\angle B_{1}
. При гомотетии с коэффициентом k=\frac{AB}{A_{1}B_{1}}
треугольник A_{1}B_{1}C_{1}
переходит в треугольник, равный треугольнику ABC
.
Решение. Пусть ABC
и A_{1}B_{1}C_{1}
— треугольники, у которых \angle A=\angle A_{1}
и \angle B=\angle B_{1}
.
Обозначим \frac{AB}{A_{1}B_{1}}=k
. Докажем, что при гомотетии с центром в произвольной точке O
и коэффициентом k
треугольник A_{1}B_{1}C_{1}
переходит в треугольник A_{2}B_{2}C_{2}
, равный треугольнику ABC
.
Действительно, так как при гомотетии с положительным коэффициентом луч переходит в сонаправленный с ним луч, то сохраняются углы, поэтому \angle A_{2}=\angle A_{1}=\angle A
и \angle B_{2}=\angle B_{1}=\angle B_{2}
. Кроме того,
A_{2}B_{2}=kA_{1}B_{1}=\frac{AB}{A_{1}B_{1}}\cdot A_{1}B_{1}=AB.
Следовательно, треугольник A_{2}B_{2}C_{2}
равен треугольнику ABC
по стороне и прилежащим к ней углам.
Треугольники A_{1}B_{1}C_{1}
и A_{2}B_{2}C_{2}
гомотетичны, значит, они подобны, а треугольники A_{2}B_{2}C_{2}
и ABC
равны и поэтому тоже подобны. Следовательно, треугольники A_{1}B_{1}C_{1}
и ABC
подобны. Утверждение доказано.