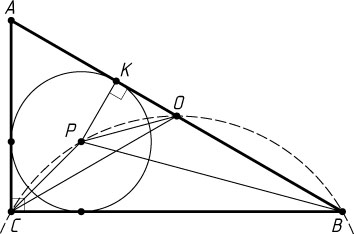
1323. В прямоугольном треугольнике ABC
угол при вершине A
равен 60^{\circ}
, O
— середина гипотенузы AB
, P
— центр вписанной окружности. Найдите угол POC
.
Ответ. 15^{\circ}
.
Указание. Точки B
, O
, P
и C
расположены на одной окружности.
Решение. Первый способ. Поскольку OC=OA
, а \angle A=60^{\circ}
, то треугольник AOC
— равносторонний, поэтому \angle BOC=120^{\circ}
. С другой стороны,
\angle BPC=90^{\circ}+\frac{1}{2}\angle A=90^{\circ}+30^{\circ}=120^{\circ}
как угол между биссектрисами углов B
и C
треугольника ABC
(см. задачу 1101). Значит, точки B
, O
, P
и C
расположены на одной окружности. Следовательно,
\angle POC=\angle PBC=15^{\circ}.
Второй способ. Поскольку OC=OA
, а \angle A=60^{\circ}
, то треугольник AOC
— равносторонний, поэтому \angle AOC=60^{\circ}
. Пусть K
— точка касания вписанной окружности с гипотенузой AB
, AB=2a
, r
— радиус вписанной окружности, p
— полупериметр треугольника ABC
. Тогда
OK=AO-AK=a-(p-BC)=a-\frac{AB+AC-BC}{2}=
=a-\frac{2a+a-a\sqrt{3}}{2}=\frac{a(\sqrt{3}-1)}{2}
(см. задачу 219),
KP=r=\frac{AC+BC-AB}{2}=\frac{a+a\sqrt{3}-2a}{2}=\frac{a(\sqrt{3}-1)}{2}
(см. задачу 217). Значит, в прямоугольном треугольнике OKP
катеты OK
и KP
равны. Следовательно, \angle KOP=45^{\circ}
, а
\angle POC=\angle AOC-\angle KOP=60^{\circ}-45^{\circ}=15^{\circ}.
Третий способ. Луч AP
— биссектриса угла при вершине A
равностороннего треугольника AOC
, значит, прямая AP
— серединный перпендикуляр к отрезку OC
, и треугольник COP
равнобедренный. Следовательно,
\angle POC=\angle OCP=\angle BCP-\angle BCO=45^{\circ}-30^{\circ}=15^{\circ}.