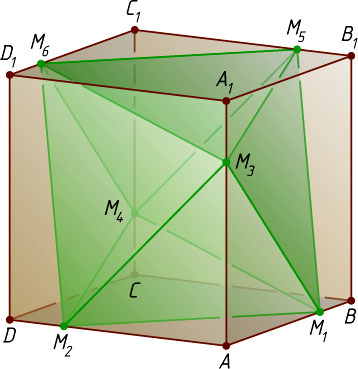
14084. Можно ли вписать правильный октаэдр в куб так, чтобы вершины октаэдра находились на рёбрах куба?
Ответ. Да, можно.
Решение. Пусть ABCDA_{1}B_{1}C_{1}D_{1}
— куб с длиной ребра 1. Отметим на рёбрах AB
, AD
, AA_{1}
, C_{1}C
, C_{1}B_{1}
, C_{1}D_{1}
точки M_{1}
, M_{2}
, M_{3}
, M_{4}
, M_{5}
, M_{6}
соответственно так, чтобы
AM_{1}=AM_{2}=AM_{3}=C_{1}M_{4}=C_{1}M_{5}=C_{1}M_{6}=\frac{3}{4}.
Тогда длины отрезков M_{1}M_{2}
, M_{2}M_{3}
, M_{3}M_{1}
, M_{4}M_{5}
, M_{5}M_{6}
, M_{6}M_{4}
равны \frac{3\sqrt{2}}{4}
, а длины отрезков M_{1}M_{4}
, M_{1}M_{5}
, M_{2}M_{4}
, M_{2}M_{6}
, M_{3}M_{5}
, M_{3}M_{6}
равны \sqrt{\left(\frac{1}{4}\right)^{2}+1^{2}+\left(\frac{1}{4}\right)^{2}}=\frac{3\sqrt{2}}{4}
.
Поскольку длины всех двенадцати отрезков равны, то все треугольники M_{1}M_{2}M_{3}
, M_{4}M_{5}M_{6}
, M_{1}M_{4}M_{5}
, M_{2}M_{4}M_{6}
, M_{3}M_{5}M_{6}
, M_{4}M_{1}M_{2}
, M_{5}M_{1}M_{3}
, M_{6}M_{2}M_{3}
равносторонние. Следовательно, точки M_{1}
, M_{2}
, M_{3}
, M_{4}
, M_{5}
, M_{6}
— вершины правильного октаэдра.