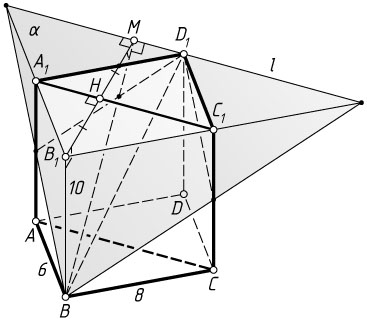
14170. В прямоугольном параллелепипеде ABCDA_{1}B_{1}C_{1}D_{1}
через диагональ BD_{1}
проведена плоскость \alpha
, параллельная прямой AC
.
а) Докажите, что прямая пересечения плоскости \alpha
с плоскостью основания A_{1}B_{1}C_{1}D_{1}
параллельна прямой A_{1}C_{1}
.
б) Найдите угол между проведённой плоскостью и плоскостью основания параллелепипеда, если AB=6
, BC=8
, CC_{1}=10
.
Ответ. \arctg\frac{25}{24}
.
Решение. а) Прямая A_{1}C_{1}
параллельна прямой AC
. Плоскость A_{1}B_{1}C_{1}D_{1}
проходит через прямую A_{1}C_{1}
, параллельную секущей плоскости, и имеет с секущей плоскостью общую точку D_{1}
, значит, прямая l
пересечения секущей плоскости \alpha
с плоскостью A_{1}B_{1}C_{1}D_{1}
параллельна прямой A_{1}C_{1}
.
б) Пусть B_{1}M
— перпендикуляр, опущенный из вершины B_{1}
на прямую l
. Тогда B_{1}M
— ортогональная проекция наклонной BM
на плоскость A_{1}B_{1}C_{1}D_{1}
. По теореме о трёх перпендикулярах BM\perp l
, поэтому угол BMB_{1}
— линейный угол двугранного угла, образованного секущей плоскостью \alpha
и плоскостью A_{1}B_{1}C_{1}D_{1}
.
Отрезок B_{1}M
вдвое больше высоты B_{1}H
прямоугольного треугольника A_{1}B_{1}C_{1}
, проведённой из вершины прямого угла, поэтому
B_{1}M=2B_{1}H=\frac{2A_{1}B_{1}\cdot B_{1}C_{1}}{A_{1}C_{1}}=\frac{2\cdot6\cdot8}{\sqrt{6^{2}+8^{2}}}=\frac{48}{5}.
Из прямоугольного треугольника BMB_{1}
находим, что
\tg\angle BMB_{1}=\frac{BB_{1}}{B_{1}M}=\frac{10}{\frac{48}{5}}=\frac{25}{24}
(см. задачу 1967). Следовательно, \angle BMB_{1}=\arctg\frac{25}{24}
.