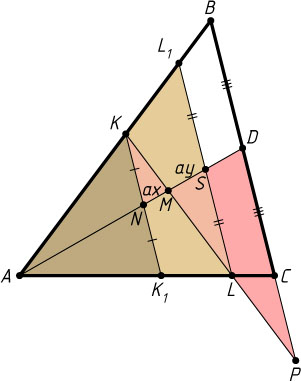
1484. Через точку M
пересечения медиан треугольника ABC
проведена прямая, пересекающая стороны AB
и AC
соответственно в точках K
и L
, а продолжение стороны BC
в точке P
(C
между P
и B
). Докажите, что \frac{1}{MK}=\frac{1}{ML}+\frac{1}{MP}
.
Решение. Пусть прямая, проходящая через точку K
параллельно стороне BC
, пересекает медиану AD
и сторону AC
в точках N
и K_{1}
соответственно, а прямая, проходящая через точку L
параллельно стороне BC
, пересекает медиану AD
и сторону AB
в точках S
и L_{1}
соответственно. Тогда NK=\frac{1}{2}KK_{1}
и LS=\frac{1}{2}LL_{1}
.
Положим MD=a
, AM=2a
, MN=ax
, MS=ay
. Треугольник AKK_{1}
подобен треугольнику AL_{1}L
, а треугольник KMN
— треугольнику LMS
, поэтому
\frac{AN}{AS}=\frac{KK_{1}}{LL_{1}}=\frac{2NK}{2LS}=\frac{NK}{LS}=\frac{MN}{MS}=\frac{x}{y},
\frac{AN}{AS}=\frac{AM-MN}{AM+MS}=\frac{2a-ax}{2a+ay}=\frac{2-x}{2+y}.
Из равенства \frac{x}{y}=\frac{2-x}{2+y}
следует, что y=\frac{x}{1-x}
.
Из подобия треугольников KMN
и LSN
следует, что
\frac{MK}{ML}=\frac{MN}{MS}=\frac{ax}{ay}=\frac{x}{y},
поэтому \frac{1}{MK}=\frac{y}{xML}
.
Из подобия треугольников PMD
и LMS
следует, что
\frac{PM}{ML}=\frac{MD}{MS}=\frac{a}{ay}=\frac{1}{y},
поэтому \frac{1}{MP}=\frac{y}{ML}
.
Следовательно, равенство \frac{1}{MK}=\frac{1}{ML}+\frac{1}{MP}
равносильно равенству \frac{y}{xML}=\frac{1}{ML}+\frac{y}{ML}
, или \frac{y}{x}=1+y
, что равносильно доказанному ранее равенству y=\frac{x}{1-x}
.