1702. Центр описанной окружности треугольника симметричен его центру вписанной окружности относительно одной из сторон. Найдите углы треугольника.
Ответ. 36^{\circ}
, 36^{\circ}
, 108^{\circ}
.
Указание. Докажите, что данный треугольник — равнобедренный; обозначьте через \alpha
его угол при основании и составьте уравнение относительно \alpha
.
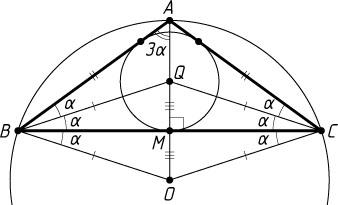
Решение. Пусть O
и Q
— соответственно центры описанной и вписанной окружностей треугольника ABC
, причём точки O
и Q
симметричны относительно прямой BC
. Обозначим \angle OBC=\angle QBC=\alpha
. Поскольку треугольник BOC
равнобедренный, то
\angle QCB=\angle OCB=\angle OBC=\alpha,
а так как BQ
— биссектриса угла ABC
, то \angle ABC=2\alpha
. Аналогично \angle ACB=2\alpha
. Значит, треугольник ABC
— равнобедренный, его биссектриса AM
является высотой, а точки Q
и M
лежат на отрезке OA
. Поскольку треугольник AOB
также равнобедренный (OA=OB
как радиусы одной окружности), то
\angle OBA=\angle OAB,~\mbox{или}~3\alpha=90^{\circ}-2\alpha.
Отсюда находим, что \alpha=18^{\circ}
. Следовательно,
\angle ACB=\angle ABC=2\alpha=36^{\circ}.