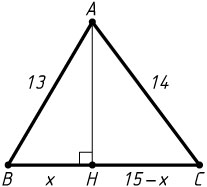
1971. Дан треугольник со сторонами 13, 14, 15. Найдите высоту, проведённую к большей стороне.
Ответ. \frac{56}{5}
.
Указание. Пусть AH
— указанная высота треугольника ABC
. Обозначьте BH=x
, CH=15-x
и выразите двумя способами AH^{2}
из прямоугольных треугольников AHB
и AHC
.
Решение. Первый способ. Пусть AH
— высота треугольника ABC
со сторонами BC=15
, AC=14
, AB=13
. Поскольку BC
— наибольшая сторона треугольника ABC
, то точка H
лежит на стороне BC
. Обозначим BH=x
. Тогда CH=BC-BH=15-x
. В прямоугольных треугольниках AHB
и AHC
AH^{2}=AB^{2}-BH^{2}=169-x^{2}~\mbox{и}~AH^{2}=AC^{2}-CH^{2}=196-(15-x)^{2}.
Из уравнения 169-x^{2}=196-(15-x)^{2}
находим, что x=\frac{33}{5}
. Следовательно,
AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{13^{2}-\left(\frac{33}{5}\right)^{2}}=\sqrt{\frac{65^{2}-33^{2}}{25}}=
=\sqrt{\frac{32\cdot98}{25}}=\frac{4\cdot7\cdot2}{5}=\frac{56}{5}.
Второй способ. Пусть AH
— указанная высота треугольника ABC
со сторонами BC=15
, AC=14
, AB=13
. По теореме косинусов
\cos\angle ABC=\frac{225+169-196}{2\cdot15\cdot13}=\frac{33}{65},
а из прямоугольного треугольника ABH
находим, что
AH=AB\sin\angle ABC=13\sqrt{1-\left(\frac{33}{65}\right)^{2}}=\frac{56}{5}.
Третий способ. Пусть AH
— указанная высота треугольника ABC
со сторонами BC=15
, AC=14
, AB=13
. По формуле Герона
S_{\triangle ABC}=\sqrt{21(21-13)(21-14)(21-15)}=\sqrt{21\cdot8\cdot7\cdot6}=7\cdot3\cdot4=84.
С другой стороны, S_{\triangle ABC}=\frac{1}{2}BC\cdot AH
. Откуда находим, что
AH=\frac{2S_{\triangle ABC}}{BC}=\frac{2\cdot84}{15}=\frac{56}{5}.