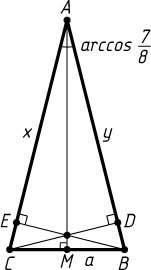
2165. В треугольнике ABC
угол A
равен \arccos\frac{7}{8}
, BC=a
, а высота, опущенная из вершины A
, равна сумме двух других высот. Найдите площадь треугольника ABC
.
Ответ. \frac{a^{2}\sqrt{15}}{4}
.
Указание. Обозначьте AC=x
, AB=y
, составьте систему уравнений и выразите из неё xy
.
Решение. Поскольку \cos\angle A=\frac{7}{8}
, то
\sin\angle A=\sqrt{1-\left(\frac{7}{8}\right)^{2}}=\frac{\sqrt{15}}{8}.
Пусть AM
, CD
и BE
— высоты треугольника ABC
. Обозначим AC=x
, AB=y
. По теореме косинусов из треугольника ABC
находим, что
BC^{2}=AC^{2}+AB^{2}-2AC\cdot AB\cos\angle A,~\mbox{или}~a^{2}=x^{2}+y^{2}-\frac{7xy}{4}.
Кроме того,
S_{\triangle ABC}=\frac{1}{2}a\cdot AM=\frac{1}{2}x\cdot BE=\frac{1}{2}y\cdot CD,~CD+BE=AM.
Из этих равенств следует, что
\frac{2S_{\triangle ABC}}{x}+\frac{2S_{\triangle ABC}}{y}=\frac{2S_{\triangle ABC}}{a},
или
\frac{1}{x}+\frac{1}{y}=\frac{1}{a}~\Leftrightarrow~a(x+y)=xy.
Из системы уравнений
\syst{x^{2}+y^{2}-\frac{7xy}{4}=a^{2}\\a(x+y)=xy\\}
находим, что xy=4a^{2}
. Следовательно,
S_{\triangle ABC}=\frac{1}{2}xy\sin\angle A=\frac{a^{2}\sqrt{15}}{4}.