2294. На сторонах прямоугольного треугольника ABC
построены во внешнюю сторону квадраты с центрами D
, E
, F
. Докажите, что отношение S_{\triangle DEF}:S_{\triangle ABC}
:
а) больше 1;
б) не меньше 2.
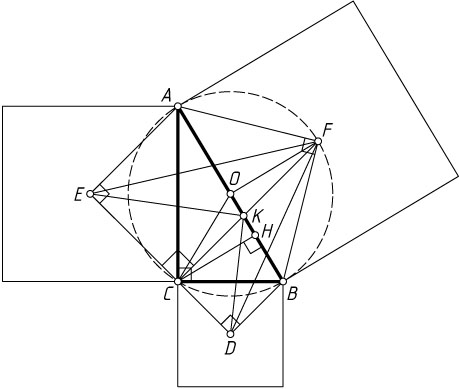
Решение. Первый способ. Пусть F
— центр квадрата, построенного на гипотенузе AB
(рис. 1), D
и E
— центры квадратов, построенных на катетах BC
и AC
соответственно, O
— середина AB
, K
— точка пересечения AB
и CF
, CH
— высота треугольника ABC
.
Диагонали квадрата перпендикулярны, поэтому \angle AFB=90^{\circ}
. Из точек C
и F
отрезок AB
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AB
. Вписанные в эту окружность углы ACF
и BCF
опираются на равные хорды AF
и BF
, поэтому они равны (см. задачу 805). Значит, CF
— биссектриса прямого угла BAC
. Точки D
, C
и E
лежат на одной прямой, так как
\angle FCE=\angle ACF+\angle ACE=45^{\circ}+45^{\circ}=90^{\circ},
\angle FCD=\angle BCF+\angle BCD=45^{\circ}+45^{\circ}=90^{\circ},
причём FC
— высота треугольника DEF
.
Прямые AE
, FC
и BD
параллельны, так как они перпендикулярны одной и той же прямой DE
, поэтому
S_{\triangle AKC}=S_{\triangle EKC},~S_{\triangle BKC}=S_{\triangle DKC}.
Тогда:
а)
S_{\triangle ABC}=S_{\triangle AKC}+S_{\triangle BKC}=S_{\triangle EKC}+S_{\triangle DKC}=
=S_{\triangle DKE}\lt S_{\triangle DEF}.
Следовательно, \frac{S_{\triangle DEF}}{S_{\triangle ABC}}\gt1
.
б)
S_{\triangle DEF}-S_{\triangle ABC}=S_{\triangle DEF}-S_{\triangle DKE}=S_{\triangle DKF}+S_{\triangle EKF}=
=S_{\triangle BKF}+S_{\triangle AKF}=S_{\triangle AFB}=\frac{1}{2}AB\cdot FO=\frac{1}{2}AB\cdot OC\geqslant\frac{1}{2}AB\cdot CH=S_{\triangle ABC},
поэтому S_{\triangle DEF}\geqslant2S_{\triangle ABC}
. Следовательно, \frac{S_{\triangle DEF}}{S_{\triangle ABC}}\geqslant2
.
Второй способ. а) Пусть BC=a
и AC=b
(рис. 2). Прямые OD
и OE
— серединные перпендикуляры к катетам BC
и AD
, поэтому, если M
— точка пересечения OD
и BC
, то
OD=OM+MD=\frac{1}{2}b+\frac{1}{2}a=\frac{a+b}{2}.
Аналогично OE=\frac{a+b}{2}
. Значит,
S_{\triangle DEF}\gt S_{\triangle DOE}=\frac{1}{2}\left(\frac{a+b}{2}\right)^{2},
а так как \sqrt{ab}\leqslant\frac{a+b}{2}
, то
S_{\triangle ABC}=\frac{1}{2}ab\leqslant\frac{1}{2}\left(\frac{a+b}{2}\right)^{2}=S_{\triangle DOE}\lt S_{\triangle DEF}.
Следовательно, \frac{S_{\triangle DEF}}{S_{\triangle ABC}}\gt1
.
б) Пусть уже доказано, что FC
— высота треугольника DEF
. Опустим перпендикуляры OL
и OP
из точки O
на ED
и FC
соответственно. Тогда OPCL
— прямоугольник, а так как OF=\frac{1}{2}AB=OC
, то треугольник COF
равнобедренный, поэтому P
— середина CF
. Значит, OL=CP=\frac{1}{2}FC
. Следовательно,
S_{\triangle DEF}=\frac{1}{2}DE\cdot FC=\frac{1}{2}DE\cdot2OL=DE\cdot OL=2S_{\triangle DOE}\geqslant2S_{\triangle ABC}
(в пункте а) доказано, что S_{\triangle DOE}\geqslant S_{\triangle ABC}
). Следовательно, \frac{S_{\triangle DEF}}{S_{\triangle ABC}}\geqslant2
.
Третий способ. Пусть F
— центр квадрата, построенного на гипотенузе AB
(рис. 3), D
и E
— центры квадратов, построенных на катетах BC
и AC
соответственно, O
— середина AB
, K
— точка пересечения AB
и CF
, CH
— высота треугольника ABC
.
Диагонали квадрата перпендикулярны, поэтому \angle AFB=90^{\circ}
. Из точек C
и F
отрезок AB
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AB
. Вписанные в эту окружность углы ACF
и BCF
опираются на равные хорды AF
и BF
, поэтому они равны (см. задачу 805). Значит, CF
— биссектриса прямого угла BAC
. Точки D
, C
и E
лежат на одной прямой, так как
\angle FCE=\angle ACF+\angle ACE=45^{\circ}+45^{\circ}=90^{\circ},
\angle FCD=\angle BCF+\angle BCD=45^{\circ}+45^{\circ}=90^{\circ},
причём FC
— высота треугольника DEF
.
Обозначим BC=a
, AB=b
, CF=x
. Пусть a\ne b
. Выражая по теореме косинусов равные отрезки AF
и BF
из треугольников ACF
и BCF
, получим уравнение x^{2}+a^{2}-ax\sqrt{2}=x^{2}+b^{2}-bx\sqrt{2}
, из которого находим, что CF=x=\frac{a+b}{\sqrt{2}}
.
Если a=b
, то AFBC
— квадрат, поэтому
CF=BC\sqrt{2}=a\sqrt{2}=\frac{a+b}{\sqrt{2}}.
Тогда
S_{\triangle DEF}=\frac{1}{2}\cdot DE\cdot CF=\frac{1}{2}\cdot\frac{a+b}{\sqrt{2}}\cdot\frac{a+b}{\sqrt{2}}=\frac{(a+b)^{2}}{4}\geqslant ab=2S_{\triangle ABC}.
Следовательно, \frac{S_{\triangle DEF}}{S_{\triangle ABC}}\geqslant2
.