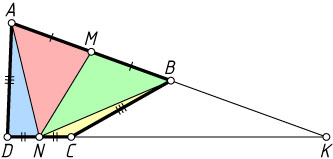
2296. Продолжения сторон AB
и CD
выпуклого четырёхугольника ABCD
пересекаются в точке K
. Известно, что AD=BC
. Пусть M
и N
— середины сторон AB
и CD
. Докажите, что треугольник MNK
— тупоугольный.
Решение. Пусть точки B
и C
лежат на отрезках AK
и DK
соответственно, M
— середина AB
, N
— середина CD
.
Сумма углов при вершинах B
и C
треугольника BCK
меньше 180^{\circ}
, поэтому сумма внешних углов треугольника при этих вершинах больше 180^{\circ}
, т. е. \angle ABC+\angle BCD\gt180^{\circ}
. Сумма углов при вершинах A
и D
треугольника AKD
меньше 180^{\circ}
, т. е. \angle MAD+\angle ADN\lt180^{\circ}
. Значит,
\angle ABC+\angle BCD\gt\angle MAD+\angle ADN.
Тогда либо \angle ABC\gt\angle MAD
, либо \angle BCD\gt\angle ADN
.
Предположим, что \angle BCD\gt\angle ADN
. Тогда две стороны BC
и CN
треугольника BCN
соответственно равны двум сторонам AD
и DN
треугольника AND
, а \angle BCN\gt\angle ADN
. Значит, BN\gt AN
(см. задачу 3606).
У треугольников MBN
и MAN
есть общая сторона MN
, BM=AM
, а BN\gt AN
. Значит, \angle BMN\gt\angle AMN
, а так как эти углы смежные, то \angle BMN\gt90^{\circ}
. Следовательно, треугольник MNK
— тупоугольный.