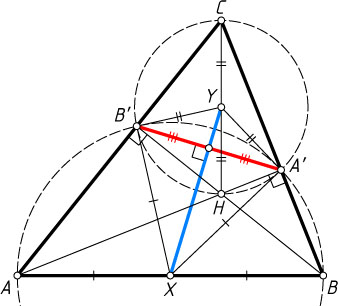
2308. Высоты AA'
и BB'
треугольника ABC
пересекаются в точке H
. Точки X
и Y
— середины отрезков AB
и CH
соответственно. Докажите, что прямые XY
и A'B'
перпендикулярны.
Решение. Первый способ. Медианы A'Y
и B'Y
прямоугольных треугольников A'CH
и B'CH
, проведённые из вершин прямых углов, равны половине общей гипотенузы CH
(см. задачу 1109). Поэтому A'Y=\frac{1}{2}CH=B'Y
. Аналогично A'X=B'X
. Значит, точки X
и Y
равноудалены от концов отрезка A'B'
. Следовательно, XY
— серединный перпендикуляр к отрезку A'B'
.
Второй способ. Из точек A'
и B'
отрезок CH
виден под прямым углом, значит, эти точки лежат на окружности с диаметром CH
. Аналогично точки A'
и B'
лежат на окружности с диаметром AB
. Точки Y
и X
— центры этих окружностей, а так как линия центров пересекающихся окружностей перпендикулярна их общей хорде, то XY\perp A'B'
.