2328. В треугольнике ABC
точка X
лежит на стороне AB
, а точка Y
— на стороне BC
. Отрезки AY
и CX
пересекаются в точке Z
. Известно, что AY=CY
и AB=CZ
. Докажите, что точки B
, X
, Z
и Y
лежат на одной окружности.
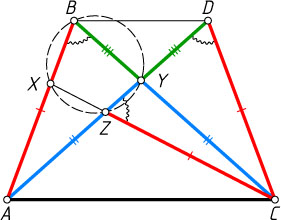
Решение. Первый способ. На продолжении отрезка AY
за точку Y
отложим отрезок YD=YB
. Тогда треугольники ABY
и CDY
равны по двум сторонам и углу между ними, поэтому CZ=AB=CD
.
Поскольку
AD=AY+YD=CY+YB=BC,
треугольники ABC
и CDA
равны по трём сторонам. Кроме того, треугольник DCZ
равнобедренный, поэтому
\angle ABC=\angle ADC=\angle ZDC=\angle DZC=180^{\circ}-\angle XZY.
Следовательно, четырёхугольник BXZY
— вписанный.
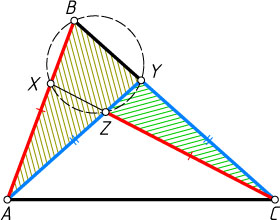
Второй способ. Применяя теорему синусов к треугольникам ABY
и CZY
, получим, что
\frac{\sin\angle ABY}{AY}=\frac{\sin\angle AYB}{AB},~\frac{\sin\angle ZYC}{CZ}=\frac{\sin\angle CZY}{CY},
а так как AY=CY
, AB=CZ
и \sin\angle AYB=\sin\angle ZYC
, то
\sin\angle ABY=\sin\angle CZY=\sin\angle XZY.
Значит, либо \angle ABY=\angle XZY
, либо \angle ABY+\angle XZY=180^{\circ}
.
Из теоремы о внешнем угле треугольника следует, что
\angle XZY\gt\angle AXZ\gt\angle ABY,
значит, \angle ABY+\angle XZY=180^{\circ}
. Следовательно, четырёхугольник BXZY
— вписанный.